
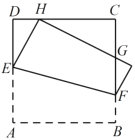
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
【答案】D
【解析】
设正方形ABCD的边长为a,CH=x,DE=y,则m=4a,根据折叠的性质可得∠EHG=∠A=90°,EH=AE,可得EH=a-y,DH=a-x,根据直角三角形两锐角互余的关系可得∠DEH=∠CHG,可证明△DEH∽△CHG,根据相似三角形的性质可用a、x、y表示出CG、HG的长,在Rt△DEH中利用勾股定理可得x2=2a(x-y),表示出△CHG的周长,进而可得答案.
设正方形ABCD的边长为a,CH=x,DE=y,则m=4a,
∵将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合,
重合,
∴∠EHG=∠A=90°,EH=AE,
∴DH=a-x,EH=a-y,
∵∠CHG+∠DHE=90°,∠DEH+∠DHE=90°,
∴∠CHG=∠DEH,
∵∠D=∠C=90°,
∴△DEH∽△CHG,
∴![]() ,即:
,即:![]() ,
,
∴CG=![]() ,HG=
,HG=![]() ,
,
在Rt△DEH中,EH2=DE2+DH2,即(a-y)2=y2+(a-x)2,
∴x2=2a(x-y),
∴n=CH+HG+CG=x+![]() +
+![]() =
=![]() =2a,
=2a,
∴![]() =
=![]() =2,
=2,
故选:D.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
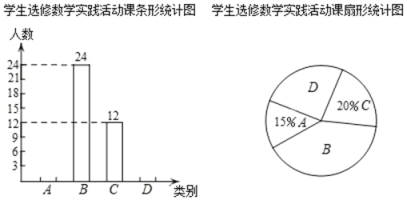
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
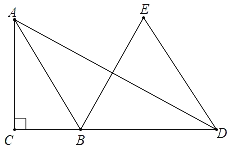
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
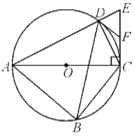
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() .
.
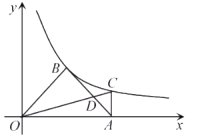
(1)求反比例函数的解析式;
(2)过点![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]() 的图像于点
的图像于点![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足k1x+b>![]() 的x的取值范围.
的x的取值范围.
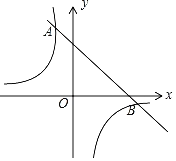
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=![]() ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE<![]() ∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,
且满足∠DBE=![]() ∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
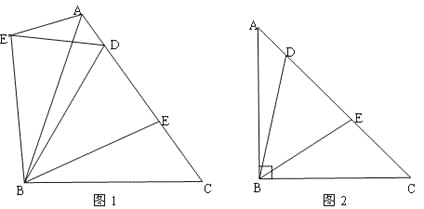
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com