
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
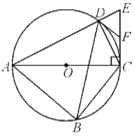
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)tan∠ABD=2.
【解析】
(1)如图,连接OD,由AC是直径可得∠ADC=90°,利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,进而得出答案;
(2)由直角三角形两锐角互余的关系可得∠DAC=∠DCE,可证明△DAC∽△DCE,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可得答案.
(1)如图,连接OD,
∵AC是⊙O直径,
∴∠ADC=90°,
∵点F为CE中点,
∴DF=CF,
∴∠FDC=∠DCF,
∵OD=OC,
∴∠ODC=∠OCD,
∵CE⊥AC,
∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是⊙O的切线.
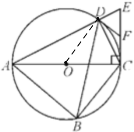
(2)∵∠OCD+∠DCF=∠DAC+∠OCD=90°,
∴∠DCF=∠DAC,
∵∠ADC=∠CDE=90°,
∴△DAC∽△DCE,
∴![]() ,即CD2=AD·DE,
,即CD2=AD·DE,
∵![]() ,
,
∴AC2=20DE2,
∵AC2=CD2+AD2,
∴AD2+AD·DE=20DE2,
∴(AD+5DE)(AD-4DE)=0,
解得:AD=4DE或AD=-5DE(舍去),
∴CD=![]() =
=![]() =2DE,
=2DE,
∵∠ABD=∠ACD,
∴tan∠ABD=tan∠ACD=![]() =
=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
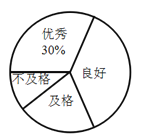
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
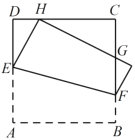
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
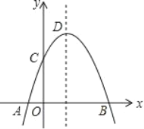
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=3;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
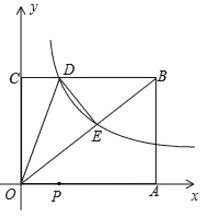
【题目】如图,已知矩形![]() 的两边OA,OC分别落在
的两边OA,OC分别落在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() 的中点E,且与BC边相交于点D.
的中点E,且与BC边相交于点D.
(1)①求反比例函数的解析式及点D的坐标;
②直接写出![]() 的面积为________.
的面积为________.
(2)若P是OA上的动点,当![]() 值为最小时,求直线
值为最小时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
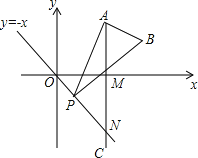
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com