
【题目】如图,抛物线![]() :
:![]() (
(![]() ,
,![]() 是常数)经过
是常数)经过![]() 、
、![]() 两点.
两点.
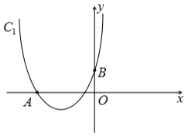
(1)求![]() ,
,![]() 的值;
的值;
(2)向右平移抛物线![]() ,使它经过点
,使它经过点![]() ,得抛物线
,得抛物线![]() ,
,![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,且在另一个交点的左侧.
,且在另一个交点的左侧.
①求抛物线![]() 的表达式;
的表达式;
②![]() 是点
是点![]() 关于抛物线
关于抛物线![]() 对称轴的对称点,
对称轴的对称点,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,
,![]() 为垂足,设
为垂足,设![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 的值,使
的值,使![]() 取得最大值.
取得最大值.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:当前,中国互联网产业发展迅速,互联网教育市场增长率位居全行业前列.以下是根据某媒体发布的2012﹣2015年互联网教育市场规模的相关数据,绘制的统计图表的一部分.
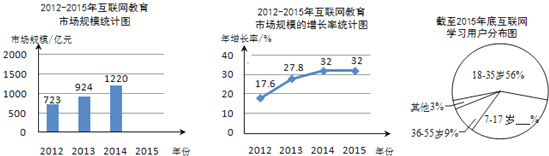
(1)2015年互联网教育市场规模约是 亿元(结果精确到1亿元),并补全条形统计图;
(2)截至2015年底,约有5亿网民使用互联网进行学习,互联网学习用户的年龄分布如图所示,请你补全扇形统计图,并估计7﹣17岁年龄段有 亿网民通过互联网进行学习;
(3)根据以上材料,写出你的思考、感受或建议(一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.
(1)求证:∠DOC=2∠G.
(2)已知⊙O的半径为3.
①若BE=2,则DA= .
②当BE= 时,四边形DOCF为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 是常数),其图象与水平直线
是常数),其图象与水平直线![]() ,
,![]() ,铅直直线
,铅直直线![]() ,
,![]() 的位置如图所示,若以其中的两条直线为
的位置如图所示,若以其中的两条直线为![]() 轴,
轴,![]() 轴所在的直线建立平面直角坐标系(向右为
轴所在的直线建立平面直角坐标系(向右为![]() 轴正方向,向上为
轴正方向,向上为![]() 轴正方向),则下列说法正确的是( )
轴正方向),则下列说法正确的是( )

A.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]() B.
B.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]()
C.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]() D.
D.![]() 轴、
轴、![]() 轴所在直线可以是直线
轴所在直线可以是直线![]() 和直线
和直线![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
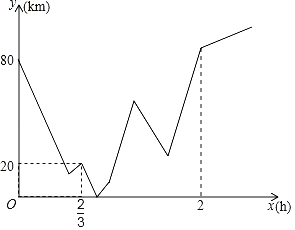
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为_____.
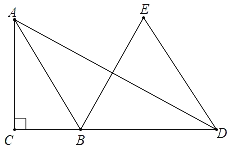
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com