
【题目】某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80. 
(1)求y关于x的函数解析式;
(2)若该种商品每千克的成本为30元,当每千克的销售价为多少元时,获得的利润为600元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE= ![]() AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是
AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个 ![]() 与
与 ![]() 的函数图像经过平移后能与某反比例函数的图像重合,那么称这个函数是
的函数图像经过平移后能与某反比例函数的图像重合,那么称这个函数是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
例如: ![]() 的图像向左平移2个单位,再向下平移1个单位得到
的图像向左平移2个单位,再向下平移1个单位得到 ![]() 的图像,则
的图像,则 ![]() 是
是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加 ![]() cm、
cm、 ![]() cm后,得到的新矩形的面积为8
cm后,得到的新矩形的面积为8 ![]() ,求
,求 ![]() 与
与 ![]() 的函数表达式,并判断这个函数是否为“反比例平移函数”.
的函数表达式,并判断这个函数是否为“反比例平移函数”.
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3) .点D是OA的中点,连接OB、CD交于点E,“反比例平移函数” ![]() 的图像经过B、E两点.则这个“反比例平移函数”的表达式为;这个“反比例平移函数”的图像经过适当的变换与某一个反比例函数的图像重合,请写出这个反比例函数的表达式 .
的图像经过B、E两点.则这个“反比例平移函数”的表达式为;这个“反比例平移函数”的图像经过适当的变换与某一个反比例函数的图像重合,请写出这个反比例函数的表达式 . 
(3)在(2)的条件下, 已知过线段BE中点的一条直线 ![]() 交这个“反比例平移函数”图像于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
交这个“反比例平移函数”图像于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在等腰△ABC中,AB=AC,F为AB边上的中点,延长CB至D,使得BD=BC,连接AD交CF的延长线于E.
(1)如图1,若∠BAC=60°,求证:△CED为等腰三角形
(2)如图2,若∠BAC≠60°,(1)中结论还成立吗?若成立,请证明,若不成立,请说明理由.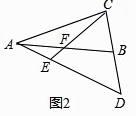
(3)如图3,当 ![]() =是(直接填空),△CED为等腰直角三角形.
=是(直接填空),△CED为等腰直角三角形.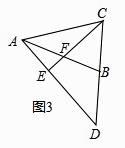
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com