
【题目】已知,在等腰△ABC中,AB=AC,F为AB边上的中点,延长CB至D,使得BD=BC,连接AD交CF的延长线于E.
(1)如图1,若∠BAC=60°,求证:△CED为等腰三角形
(2)如图2,若∠BAC≠60°,(1)中结论还成立吗?若成立,请证明,若不成立,请说明理由.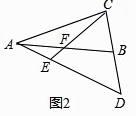
(3)如图3,当 ![]() =是(直接填空),△CED为等腰直角三角形.
=是(直接填空),△CED为等腰直角三角形.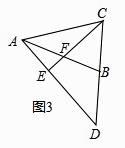
【答案】
(1)
证明:如图1,
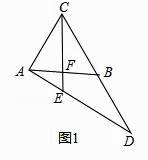
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,AB=BC,
而BC=BD,
∴AB=BD,
∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,
∴∠D=30°,
∵F点AB的中点,
∴CF平分∠ACB,
∴∠ACE=∠DCE=30°,
∴∠D=∠DCE,
∴△CED为等腰三角形;
(2)
解:成立.
延长CF到M使FM=CF,连接AM,如图2,

在△AMF和△BCF中
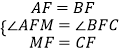 ,
,
∴△AMF≌△BCF,
∴AM=BC,∠M=∠BCF,
∵BC=BD,
∴AM=BD,
∵∠M=∠BCF,
∴AM∥CD,
∴∠MAC+∠ACB=180°,
而∠DBA+∠ABC=180°,∠ABC=∠ACB,
∴∠MAC=∠DBA,
在△AMC和△BDA中
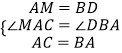 ,
,
∴△AMC≌△BDA,
∴∠M=∠D,
∴∠D=∠DCE,
∴△CED为等腰三角形;
(3)![]()
【解析】(3)解:作BH⊥CE于H,连接BE,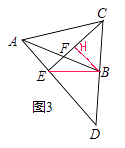
由(2)得△CED为等腰三角形,当∠BCE=45°时,△CED为等腰直角三角形,
∴EB⊥CD,
设BH=x,则CH=EH=x,BC= ![]() x,
x,
易证得△AEF≌△BHF,则EF=HF= ![]() HE=
HE= ![]() x,
x,
在△BFH中,BF= ![]() =
= ![]() x,
x,
∴AB=2BF= ![]() x,
x,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案为 ![]() .
.
(1)如图1,先证明△ABC为等边三角形得到∠ACB=∠ABC=60°,AB=BC,再证明∠D=∠DCE=30°,然后根据等腰三角形的判定定理得到△CED为等腰三角形;(2)延长CF到M使FM=CF,连接AM,如图2,先证明△AMF≌△BCF得到AM=BC,∠M=∠BCF,再证明△AMC≌△BDA得到∠M=∠D,所以∠D=∠DCE,于是可判断△CED为等腰三角形;(3)作BH⊥CE于H,连接BE,如图3,由(2)得△CED为等腰三角形,当∠BCE=45°时,△CED为等腰直角三角形,则EB⊥CD,设BH=x,则CH=EH=x,BC= ![]() x,易证得△AEF≌△BHF,则EF=HF=
x,易证得△AEF≌△BHF,则EF=HF= ![]() HE=
HE= ![]() x,再利用勾股定理计算出BF=
x,再利用勾股定理计算出BF= ![]() x,所以AB=2BF=
x,所以AB=2BF= ![]() x,然后计算出
x,然后计算出 ![]() 的值.
的值.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2= ![]() 的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=
的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE= ![]() .
. 
(1)求反比例函数的解析式;
(2)求证:S△AOC=2S△BOC;
(3)直接写出当y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80. 
(1)求y关于x的函数解析式;
(2)若该种商品每千克的成本为30元,当每千克的销售价为多少元时,获得的利润为600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题: 
(1)这四个班共植树棵;
(2)补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级所种植的树成活了190棵,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“校园文化节“活动,对学生参加书法比赛的作品按A、B、C、D四个等级进行了评定.现随机抽取部分参赛学生书法作品的评定结果进行统计分析,并将分析结果绘制成如图扇形统计图(图①)和条形统计图(图②),根据所给信息完成下列问题: 
(1)本次抽取的样本的容量为;
(2)在图①中,C级所对应的扇形圆心角度数是;
(3)请在图②中将条形统计图补充完整;
(4)已知该校本次活动学生参赛的书法作品共750件,请你估算参赛作品中A级和B级作品共多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣ ![]() ,3),反比例函数y=
,3),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( ) 
A.4 ![]()
B.﹣4 ![]()
C.2 ![]()
D.﹣2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com