
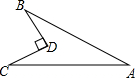
 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积. 分析 连接BC,根据已知条件运用勾股定理求得BC,运用勾股定理逆定理可证△ABC为直角三角形,然后代入三角形面积公式将两直角三角形的面积求出来,两者面积差即为四边形ABDC的面积
解答 解:如图,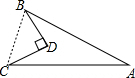
连接BC,
∵BD⊥DC,
∴∠D=90°,
∴△DBC为直角三角形,
∵BC2=BD2+CD2=82+62=102,
∴AC=10,
在△ABC中,
∵AB2+BC2=100+576=676,AC2=262=676,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,且∠ABC=90°,
∴S四边形ABDC=S△ABC-S△BCD=$\frac{1}{2}$×10×24-$\frac{1}{2}$×6×8=96.
点评 此题考查了勾股定理和勾股定理的逆定理,通过作辅助线可将一般的四边形转化为两个直角三角形,使面积的求解过程变得简单.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:解答题
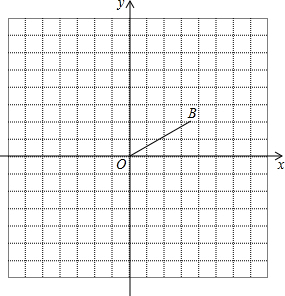 如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.
如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B. →装入不透明的甲袋
→装入不透明的甲袋 →装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
→装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 | B. | 10 | C. | 20 | D. | 5$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com