练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．在直角三角形ABC中，已知∠C=90°，∠A=60°，AC=10$\sqrt{3}$，则BC等于（　　）
    A．30B．10C．20D．5$\sqrt{3}$

    分析 先求出∠B=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2AC，然后利用勾股定理求出BC即可．

    解答 解：∵∠C=90°，∠A=60°，
    ∴∠B=90°-60°=30°，
    ∴AB=2AC=20$\sqrt{3}$，
    由勾股定理得：BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{（20\sqrt{3}）^{2}-（10\sqrt{3}）^{2}}$=30．
    故选：A．

    点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半、勾股定理；熟练掌握勾股定理，由直角三角形30°角所对的直角边等于斜边的一半求出AB是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．（1）计算：-12016+18$÷（-3）×|-\frac{1}{2}|$
    （2）先化简，再求值：3（x2+xy-1）-（3x2-2xy），其中x=1，y=-$\frac{1}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．一次函数y=2x+16分别交x轴、y轴与点M、N，且P在第二象限内位于直线MN左侧的一个动点，△MNP正好构成一个以MN为直角边的等腰直角三角形．
    （1）求P点的坐标；
    （2）在直线x=-1上存在点Q，使得S△MNQ=S△MNP，请求出Q点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，四边形ABDC，BD⊥CD，BD=6，CD=8，AB=24，AC=26，求该四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点P（-1，1），则k的值是（　　）
    A．0B．-2C．2D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某校开展了主题为“梅山文化知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了不完整的表格和扇形统计图（如图）．
    等级非常了解比较了解基本了解不太了解
    频数50m4020
    根据以上提供的信息解答下列问题：
    （1）本次问卷调查共抽取的学生数为200人，表中m的值为90；
    （2）计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数，并补全扇形统计图；
    （3）若该校有学生2000人，请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

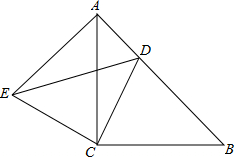    15．如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点．
    （1）求证：△BCD≌△ACE；
    （2）若AE=8，DE=10，求AB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．点A（0，-3），点B（0，-4），点C在x轴上，如果△ABC的面积为15，则点C的坐标是（30，0）或（-30，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图是一个“中”的几何体，则该几何体的俯视图为（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案