
分析 (1)作PS⊥坐标轴于S.通过证得△PMS≌△MNO(AAS),得到PS=OM=8,SM=NO=16,即可求得P的坐标.
(2)根据同底等高的三角形面积相等,只要求得直线P1P2与直线x=-1的交点即可,从而求得符合题意的Q点的坐标.
解答 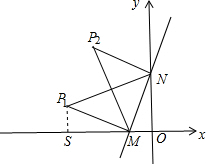 解:(1)如图,作PS⊥坐标轴于S.
解:(1)如图,作PS⊥坐标轴于S.
∵一次函数y=2x+16分别交x轴、y轴与点M、N,
∴M(-8,0),N(0,16),
∵△MNP是以MN为直角边的等腰直角三角形.
∴PM=MN,∠PMN=90°,
∴∠PMS=∠MNO,
在△PMS和△MNO中,
$\left\{\begin{array}{l}{∠PMS=∠MNO}\\{∠PSM=∠MON=90°}\\{PM=MN}\end{array}\right.$,
∴△P1MS≌△MNO(AAS),
∴P1S=OM=8,SM=NO=16,
∴P1(-24,8)
同理证得P2(-16,24),
∴P(-24,8)或(-16,24);
(2)∵P1(-24,8),P2(-16,24),
∴直线P1P2的解析式为y=2x+56,
把x=-1代入得,y=-2+56=54,
∴Q1(-1,54),此时S△MNQ=S△MNP,
∵直线x=-1与MN交于(-4,8),
∴Q2(-1,-38).
故出Q点坐标为(-1,54)或(-1,-38).
点评 本题考查了一次函数图象上点的坐标特征,三角形全等的判定和性质,还考查了等腰直角三角形的性质,要熟练掌握.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
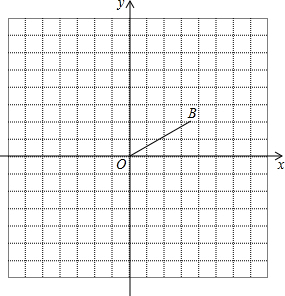 如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.
如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B. →装入不透明的甲袋
→装入不透明的甲袋 →装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
→装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 | B. | 10 | C. | 20 | D. | 5$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com