
科目:初中数学 来源: 题型:解答题
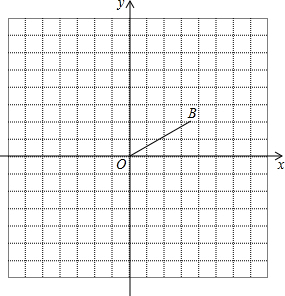 如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B.
如图,在平面直角坐标系中,点B的坐标是(2$\sqrt{3}$,2),将线段OB绕点O顺时针旋转120°,点B的对应点是点B. →装入不透明的甲袋
→装入不透明的甲袋 →装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
→装入不透明的乙袋,李南从甲袋中,王易从乙袋中,各自随机地摸出一个球(不放回),把李南摸出的球的编号作为横坐标x,把王易摸出的球的编号作为纵坐标y,用列表法或画树状图法表示出(x,y)的所有可能出现的结果;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 | B. | 10 | C. | 20 | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
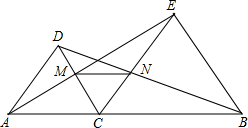 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com