
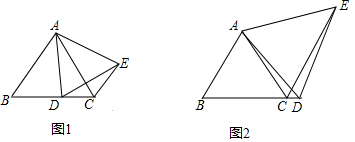
分析 (1)结论:AB∥CE,BD=CE.只要证明△BAD≌△CAE即可.
(2)若点D在BC的延长线上,则(1)中的两个结论成立.证明方法类似.
(3)分两种情形讨论,如图3中,作AF⊥BC于F.如图3中,作AF⊥BC于F,在Rt△ADF中,根据DE=AD=$\sqrt{A{F}^{2}+D{F}^{2}}$计算即可.
(4)由题意四边形ABDE的面积是△ABC面积的$\frac{13}{4}$倍,点D只有在BD的延长线上时,如图3右图中,设BC=2a,CD=ka,则AF=$\sqrt{3}$a,AD=$\sqrt{3{a}^{2}+(a+ka)^{2}}$,可得S四边形ABDE=S△ABD+S△AED=$\frac{1}{2}$•(2a+Ka)•$\sqrt{3}$a+$\frac{\sqrt{3}}{4}$•[3a2+(a+ka)2],S△ABC=$\frac{\sqrt{3}}{4}$•(2a)2=$\sqrt{3}$a2,由题意$\frac{1}{2}$•(2a+Ka)•$\sqrt{3}$a+$\frac{\sqrt{3}}{4}$•[3a2+(a+ka)2]=$\frac{13}{4}$•$\sqrt{3}$a2,
整理得k2+4k-5=0,解得k=1,由此即可解决问题.
解答 解:(1)如图1中,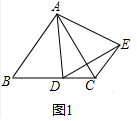
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠BAC=∠B=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴BD=CE,∠ACE=∠B=60°,
∴∠BAC=∠ACE,
∴AB∥CE,
故答案为AB∥CE,BD=CE.
(2)若点D在BC的延长线上,则(1)中的两个结论成立.
理由:如图2中,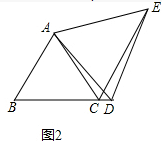
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠BAC=∠B=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴BD=CE,∠ACE=∠B=60°,
∴∠BAC=∠ACE,
∴AB∥CE,
(3)如图3中,作AF⊥BC于F.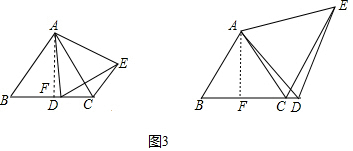
①当点D在线段BC上时,在Rt△ADF中,易知AD=3$\sqrt{3}$,DF=1,DE=AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{1}^{2}}$=2$\sqrt{7}$.
②当点D在线段BC的延长线上时,在Rt△ADF中,易知AD=3$\sqrt{3}$,DF=5,如图3中,作AF⊥BC于F.
$\sqrt{(3\sqrt{3})^{2}+{5}^{2}}$=2$\sqrt{13}$.
(4)由题意四边形ABDE的面积是△ABC面积的$\frac{13}{4}$倍,点D只有在BD的延长线上时,如图3右图中,设BC=2a,CD=ka,则AF=$\sqrt{3}$a,AD=$\sqrt{3{a}^{2}+(a+ka)^{2}}$,
∴S四边形ABDE=S△ABD+S△AED=$\frac{1}{2}$•(2a+Ka)•$\sqrt{3}$a+$\frac{\sqrt{3}}{4}$•[3a2+(a+ka)2],
∵S△ABC=$\frac{\sqrt{3}}{4}$•(2a)2=$\sqrt{3}$a2,
由题意$\frac{1}{2}$•(2a+Ka)•$\sqrt{3}$a+$\frac{\sqrt{3}}{4}$•[3a2+(a+ka)2]=$\frac{13}{4}$•$\sqrt{3}$a2,
整理得k2+4k-5=0,解得k=1,k=-5(舍),
∴tan∠ADB=$\frac{AF}{DF}$=$\frac{\sqrt{3}a}{2a}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查三角形综合题、等边三角形的性质、勾股定理、全等三角形的判定和性质、一元二次方程等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
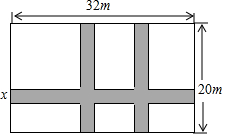 如图,在长为32m,宽为20m的矩形空地内,修三条同样宽的道路(阴影部分的矩形为空地内的道路),所修的道路将这块空地分成六块,如果在空地上道路以外的部分种上花草,并且保证种花草的面积是570m2,问道路应多宽?设道路的宽为xm,则下面所列方程正确的是( )
如图,在长为32m,宽为20m的矩形空地内,修三条同样宽的道路(阴影部分的矩形为空地内的道路),所修的道路将这块空地分成六块,如果在空地上道路以外的部分种上花草,并且保证种花草的面积是570m2,问道路应多宽?设道路的宽为xm,则下面所列方程正确的是( )| A. | (32-x)(20-x)=32×20-570 | B. | 32x+2×20x=32×20-570 | ||
| C. | (32-2x)(20-x)=570 | D. | 32x+2×20x-2x2=570 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com