
分析 先把括号内通分,再把除法运算化为乘法运算,约后后得到$\frac{1}{x+3}$,然后把x的值代入计算即可.
解答 解:$\frac{{x}^{2}-9}{{x}^{2}-3x}$÷(6+$\frac{{x}^{2}+9}{x}$),
=$\frac{{x}^{2}-9}{{x}^{2}-3x}$÷$\frac{6x+{x}^{2}+9}{x}$,
=$\frac{(x+3)(x-3)}{x(x-3)}$•$\frac{x}{(x+3)^{2}}$,
=$\frac{1}{x+3}$;
当x=$\sqrt{3}$-1时,原式=$\frac{1}{\sqrt{3}-1+3}$=$\frac{1}{\sqrt{3}+2}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$.
点评 本题考查了分式的化简求值:先把分式的分子或分母因式分解,再进行通分或约分,得到最简分式或整式,然后把满足条件的字母的值代入计算得到对应的分式的值.


科目:初中数学 来源: 题型:选择题
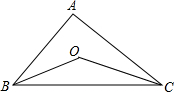 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )| A. | 140° | B. | 120° | C. | 90° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
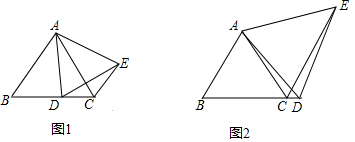
 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )| A. | 1.5 | B. | 2.5 | C. | 2.25 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com