
【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

【答案】(1)证明见解析;(2)QF=5.
【解析】试题分析:(1)首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可证明AE⊥BF;(2)由△BCF沿BF对折,得到△BPF可得FP=FC,∠PFB=∠BFC,∠FPB=90,在利用角的关系求出QF=QB,设设QF=x,在Rt△BPQ中,利用勾股定理可建立关于x的方程解方程求出x的值即可.
试题解析:(1)∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,
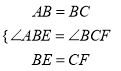
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF;
(2)∵将△BCF沿BF折叠,得到△BPF,
∴FP=FC,∠PFB=∠BFC,∠FPB=90°,
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
设QF=x,PB=BC=AB=4,CF=PF=2,
∴QB=x,PQ=x﹣2,
在Rt△BPQ中,∴x2=(x﹣2)2+42,
解得:x=5,
即QF=5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在南宁市举行的“中国东盟贸易博览会”中,贵港市的外贸成交额接近31300万元人民币,用科学记数法表示这个数据(单位:万元),正确的是( )
A.3.13×104
B.3.13×103
C.31.3×103
D.31.3×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国国际航空公司规定头等舱旅客可以免费托运不超过40千克的行李,超过部分每千克收取15元的托运费,某旅客需交的托运费为225元,那么他托运的行李重量为__________千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线向上平移2个单位长度,再向右平移3个单位长度后得到y=﹣(x﹣2)2+3,则原抛物线的解析式为( )
A.y=﹣(x+1)2+1B.y=﹣(x﹣1)2﹣1
C.y=﹣x2D.y=﹣(x﹣5)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2向上平移2个单位后,所得的抛物线的函数表达式为( )
A.y=x2+2
B.y=x2﹣2
C.y=(x+2)2
D.y=(x﹣2)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com