
分析 (1)根据整式的乘法进行化简即可,然后将题目中的x的值代入化简结果即可求得最终问题的值.
(2)根据整式的乘法进行化简即可,然后将题目中的x的值代入化简结果即可求得最终问题的值.
(3)根据幂的乘方,整式的乘法进行化简即可,然后将题目中的x的值代入化简结果即可求得最终问题的值.
解答 解:(1)x(x2-4)-(x+3)(x2-3x+2)-2x(x-2)
=x3-4x-(x3-7x+6)-(2x2-4x)
=x3-4x-x3+7x-6-2x2+4x
=-2x2+7x-6.
当x=$\frac{3}{2}$时,原式=-2×$(\frac{3}{2})^{2}+7×\frac{3}{2}-6$=0.
(2)(x-2)(x-3)+2(x+6)(x-5)-3(x2-7x+13)
=(x2-5x+6)+2(x2+x-30)-(3x2-21x+39)
=x2-5x+6+2x2+2x-60-3x2+21x-39
=18x-93.
当x=$3\frac{1}{2}$时,原式=18×$3\frac{1}{2}-93=63-93=-30$.
(3)yn(yn+9y-12)-3(3yn-1-4yn)
=y2n+9yn+1-12yn-9yn-1+12yn
=y2n+9yn+1-9yn-1.
当y=-3,n=2时,原式=(-3)2×2+9×(-3)2+1-9×(-3)2-1=-135.
点评 本题考查整式的混合运算--化简并且求值,解题的关键是去括号时注意括号内的各项的符号是否改变.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
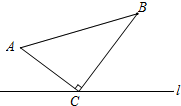 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com