练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将7张如图1所示的长为a，宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内，未被覆盖的部分(两个长方形)用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，求a，b满足的条件．

    【答案】a=3b

    【解析】

    表示出左上角与右下角部分的面积，求出之差，根据差与BC无关即可求出a与b的关系式．

    左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a，

    ∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，

    ∴AE+a=4b+PC，即AE-PC=4b-a，

    ∴阴影部分面积之差S=AEAF-PCCG=3bAE-aPC=3b（PC+4b-a）-aPC=（3b-a）PC+12b2-3ab，

    则3b-a=0，即a=3b．

    故答案为：a=3b．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】把下列各数分类

    ﹣3，0.45， ，0，9，﹣1，﹣1，10，﹣3.14

    （1）正整数：{　　…}

    （2）负整数：{　　…}

    （3）整数：{　　…}

    （4）分数：{　　 …}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果∠A和∠B互补，且∠A＞∠B，给出下列四个式子：①90°﹣∠B；②∠A﹣90°；③（∠A+∠B）④（∠A﹣∠B）其中表示∠B余角的式子有_____．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

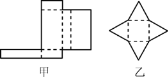
    【题目】观察图，回答下列问题：

    (1)甲、乙两图分别能折成什么几何体？简述它们的特征；

    (2)设几何体的面数为F，顶点数为V，棱数为E，请计算(1)中两个几何体的F＋V－E的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点（﹣1，y1），（4，y2）在一次函数y=3x﹣2的图象上，则y1 ， y2 ， 0的大小关系是（ ）
    A.0＜y1＜y2
    B.y1＜0＜y2
    C.y1＜y2＜0
    D.y2＜0＜y1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次“构造勾股数”的探究性学习中，老师给出了下表：

    其中、为正整数，且．

    （）观察表格，当， 时，此时对应的、、的值能否为直角三角形三边的长？说明你的理由．

    （）探究， ， 与、之间的关系并用含、的代数式表示： __________， __________， __________．

    （）以， ， 为边长的三角形是否一定为直角三角形？如果是，请说明理由；如果不是，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．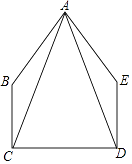

    （1）求证：△ABC≌△AED；
    （2）当∠B=140°时，求∠BAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．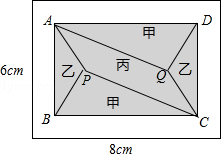

    （1）若区域Ⅰ的三种瓷砖均价为300元/m2 ， 面积为S（m2），区域Ⅱ的瓷砖均价为200元/m2 ， 且两区域的瓷砖总价为不超过12000元，求S的最大值；
    （2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
    ①求AB，BC的长；
    ②若甲、丙两瓷砖单价之和为300元/m2 ， 乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD=CD，∠ABD=∠ACD=90°，点E、F分别在AB、AC上，若ED平分∠BEF．

    （1）求证：FD平分∠EFC．

    （2）若EF=4，AF=6，AE=5，求BE和CF的和的长．

    查看答案和解析>>

    同步练习册答案