【题目】某校要举办国庆联欢会，主持人站在舞台的黄金分割点处最自然得体．如图，若舞台AB的长为20m，C为AB的一个黄金分割点（AC＜BC），则AC的长为（结果精确到0.1m）（ ）
A.6.7m
B.7.6m
C.10m
D.12.4m
科目：初中数学 来源： 题型：
【题目】先化简，再求值：a+
，其中a=1007.如图是小亮和小芳的解答过程.
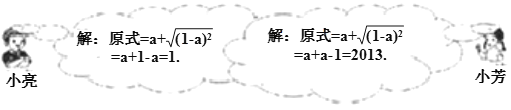
(1)_________的解法是错误的；
(2)错误的原因在于未能正确地运用二次根式的性质：_________；
(3)先化简，再求值：a+2
，其中a=-2007.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C在⊙O上，∠CAB的平分线交⊙O于点D，过点D作AC的垂线交AC的延长线于点E，连接BC交AD于点F．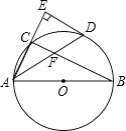
（1）猜想ED与⊙O的位置关系，并证明你的猜想；
（2）若AB=6，AD=5，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
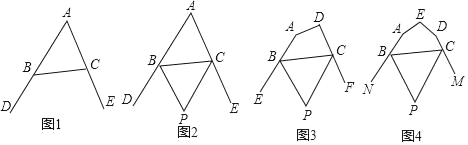
【题目】（1）如图1，在△ABC中，∠DBC与∠ECB分别为△ABC的两个外角，若∠A＝60°，∠DBC+∠ECB多少度；
（2）如图2，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有怎样的数量关系？为什么？
（3）如图3，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A+∠D有怎样的数量关系？为什么？
（4）如图4，在五边形ABCDE中，BP、CP分别平分外角∠NBC、∠MCB，∠P与∠A+∠D+∠E有怎样的数量关系？(直接写出答案)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下列解题过程，然后回答问题：
解方程： 
解：①当
≥0时，原方程可化为： 
，解得
；
②当
＜0时，原方程可化为： 
，解得
；
所以原方程的解是
或
（1）解方程： 
（2）探究：当
为何值时，方程
①无解；②只有一个解；③有两个解。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，对称轴为直线x=﹣1，与x轴的一个交点为（1，0），与y轴的交点为（0，3），则方程ax2+bx+c=0（a≠0）的解为（ ）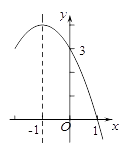
A.x=1
B.x=﹣1
C.x1=1，x2=﹣3
D.x1=1，x2=﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，AB=4cm，点E、F同时从C点出发，以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动，到点A时停止运动．设运动时间为t（s），△AEF的面积为S（cm2），则S（cm2）与t（s）的函数关系可用图象表示为（ ）
A.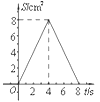
B.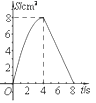
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1.5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．
（1）这项工程的规定时间是多少天？
（2）已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
