
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )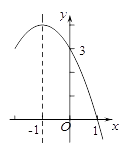
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4
【答案】C
【解析】∵抛物线的对称轴为直线x=﹣1,与x轴的一个交点为(1,0),
∴抛物线与x轴另一个交点坐标为(﹣3,0).
∴ax2+bx+c=0(a≠0)的解为x1=1,x2=﹣3.
所以答案是:C.
【考点精析】关于本题考查的二次函数的性质和抛物线与坐标轴的交点,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某公司以每吨![]() 元的价格收购了
元的价格收购了![]() 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是![]() 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 (元/吨) |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在![]() 天内将这批药材加工完毕.
天内将这批药材加工完毕.
(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好![]() 天完成,求可获利多少元?
天完成,求可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6cm,AC=12cm,动点D以1cm/s 的速度从点A出发到点B止,动点E以2cm/s 的速度从点C出发到点A止,且两点同时运动,当以点A、D、E为顶点的三角形与△ABC相似时,求运动的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )![]()
A.6.7m
B.7.6m
C.10m
D.12.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 . 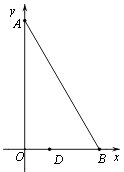
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法,正确的是( )
A. 若ac=bc,则a=b
B. 30.15°=30°15′
C. 一个圆被三条半径分成面积比2:3:4的三个扇形,则最小扇形的圆心角为90°
D. 钟表上的时间是9点40分,此时时针与分针所成的夹角是50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com