
如图,已知Rt△ABC中,∠C=90°,AC=8,BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都停止运动,设点P,Q运动的时间为t秒.
(1)在运动过程中,求P,Q两点间距离的 最大值;
最大值;
(2)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式;
(3)P,Q两点在运动过程中,是否存在时间t,使得△PQC为等腰三角形?若存在,求出此时的t值;若不存在,请说明理由(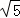 ≈2.24,结果保留一位小数)
≈2.24,结果保留一位小数)
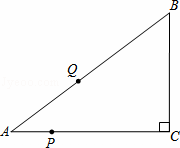
解:(1)如图1,过Q作QE⊥AC于E,连接PQ,
∵∠C=90°,
∴QE∥BC,
∴△ABC∽△AQE,
∴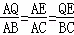 ,
,
∵AQ=2t,AP=t,
∵∠C=90°,AC=8,BC=6,
∴AB=10,
∴ ,
,
∴PE=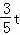 ,QE=
,QE= ,
,
∴PQ2=QE2+PE2,
∴PQ=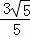 t,
t,
当Q与B重合时,PQ的值最大,
∴当t=5时,PQ的最大值=3 ;
;
(2)如图1,△ABC被直线PQ扫过的面积 =S△AQP,
=S△AQP,
当Q在AB边上时,S= AP•QE=
AP•QE= t•
t•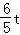 =
= ,(0<t≤5)
,(0<t≤5)
当Q在BC边上时,△ABC被直线PQ扫过的面积=S四边形ABQP,
∴S四边形ABQP=S△ABC﹣S△PQC=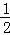 ×8×6﹣
×8×6﹣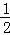 (8﹣t)•(16﹣2t)=﹣t2+16t﹣40,(5<t≤8);
(8﹣t)•(16﹣2t)=﹣t2+16t﹣40,(5<t≤8);
∴经过t秒的运动,△ABC被直线PQ扫过的面积S与时间t的函数关系式:S= 或S=﹣t2+16t﹣40.
或S=﹣t2+16t﹣40.
(3)存在,如图2,连接CQ,PQ,
由(1)知QE=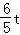 ,CE=AC﹣AE=8﹣
,CE=AC﹣AE=8﹣ ,PQ=
,PQ=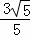 t,
t,
∴CQ= =
= =
= =2
=2 ,
,
①当CQ=CP时,
即:2 =8﹣t,
=8﹣t,
解得;t= ,
,
②当PQ=CQ时,
即;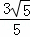 t=2
t=2 ,
,
解得:t=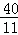 ,t=
,t= (不合题意舍去),
(不合题意舍去),
③当PQ=PC时,
即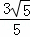 t=8﹣t,
t=8﹣t,
解得:t=3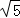 ﹣5≈1.7;
﹣5≈1.7;
综上所述:当t=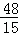 ,t=
,t=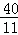 ,t=1.7时,△PQC为等腰三角形.
,t=1.7时,△PQC为等腰三角形.




科目:初中数学 来源: 题型:
为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流 密度x的一次函数.
密度x的一次函数.
(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密 度在什么范围内?
度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20 ≤x≤220时,求彩虹桥上车流量y的最大值.
≤x≤220时,求彩虹桥上车流量y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )

A. k>0,b>0 B. k<0,b<0 C. k<0,b>0 D. k>0,b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
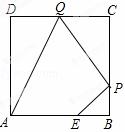
如图,已知正方形ABCD边长为3,点E在AB边上且 BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com