
����Ŀ���Ķ����ϣ���ش��������⣮
����һ���ҹ��Ŵ���ѧ���ؾ����ڡ�������¡��м����ˡ���б�������������֪�����ε����߳�����������������ִ�ʽ�ӱ�ʾ��Ϊ�� �٣�����
�٣�����![]() Ϊ�����ε����߳���
Ϊ�����ε����߳���![]() Ϊ�����������һ�������Ź���ϣ��Ҳ��������������ġ�����ʽ����
Ϊ�����������һ�������Ź���ϣ��Ҳ��������������ġ�����ʽ����![]() �����ڣ�����
�����ڣ�����![]() ��
��
���϶�������ƽ���ʽ��![]() ��ʽ���ÿɵã�
��ʽ���ÿɵã�![]() ������
������![]()
��1������֪�����ε����߳��ֱ�Ϊ4��5��7����ֱ����ù�ʽ�ٺ�ʽ�ڣ�����������ε������
��2�����ܷ��ɹ�ʽ���Ƶ�����ʽ�ڣ������ԣ�д���Ƶ����̣�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,��A,B������ֱ�Ϊ(1,0),(3,0)����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD.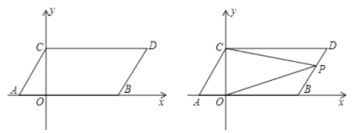
(1)���C,D�����꼰�ı���ABDC�����S�ı���ABDC��
(2)��y�����Ƿ����һ��P,����PA,PB,ʹS��PAB=S�ı���ABDC?����������һ�㣬�����P�����ꣻ�������ڣ���˵�����ɣ�
(3)��P��ֱ��BD��һ�����㣬����PC��PO������P��ֱ��BD���˶�ʱ����ֱ��д����OPC���PCD����POB��������ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬����
Ϊ����ԭ�㣬����![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ����ֱ��ڵ�һ���͵�������.ֱ��
����ֱ��ڵ�һ���͵�������.ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��

��1����ͼ1�����![]() �����ꣻ
�����ꣻ
��2����ͼ2��![]() Ϊ����
Ϊ����![]() ��һ���㣨�����
��һ���㣨�����![]() �͵�
�͵�![]() �غϣ�������
�غϣ�������![]() ��
��![]() �ύֱ��
�ύֱ��![]() �ڵ�
�ڵ�![]() .���߶�
.���߶�![]() �ij���Ϊ
�ij���Ϊ![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ����ֱ��д���Ա���
�ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ͼ3���ڣ�2���������£�����![]() �˶����߶�
�˶����߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ���Ľ�ƽ����
���Ľ�ƽ����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ij������AC�ϣ�����һ��������BC��վ�ڵ�F���������������B������Ϊ300������������ǰ��20�����E���������������B������Ϊ600������������BC�ij�.��![]() �������ȷ��0.1�ף�
�������ȷ��0.1�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
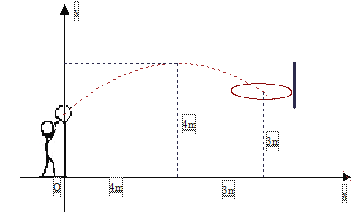
����Ŀ�������꼶��һ����������У���ͼ��Ա������Ͷ������֪�����ʱ������![]() m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
��1��������ͼ��ʾ��ƽ��ֱ������ϵ���������ߵĽ���ʽ���жϴ����ܷ�ȷͶ�У�
��2����ʱ�����Է���Ա���ڼ�ǰ��1m�������ñ���أ���֪�ҵ��������Ϊ3.1m����ô���ܷ��óɹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
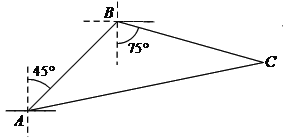
����Ŀ����ͼ����ֹ�����ڼ䣬ij���ϻ������ij����Ѳ�ߣ�����ijһʱ����A���ӵ�ָ�Ӳ�֪ͨ�������Ƕ����������12�����B����һ�Ҳ��㴬����������ƫ��75�㷽����ÿСʱ10������ٶȺ��У������Ա��������Ѳ�ߴ���ÿСʱ14������ٶ��ر�ƫ��ijһ�����������C���ɹ����ز��㴬����Ѳ�ߴ��ӳ������ɹ����ز��㴬���õ�ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() �����ۣ���
�����ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�����У� ��
��������ȷ�����У� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+2x��3��
��1������㷨����y=x2+2x��3��ͼ��
��2��������������ͼ��ش����⣺��x�� ��ʱ������ֵy��x�����������x�� ��ʱ������ֵy��x���������С��
�⣺�б��ã�
X | |||||||
Y |
��㡢����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
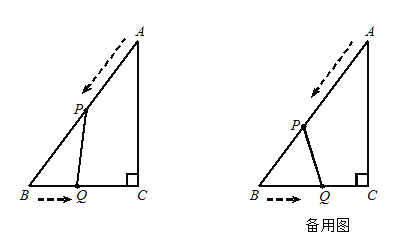
����Ŀ����ͼ12���ڡ�ABC�У���C=90����AB=10cm��BC=6cm. ��P�ӵ�A��������AB����2 cm/s���ٶ����B�����ƶ�����Q�ӵ�B��������BC����1 cm/s���ٶ����C�����ƶ�. ��һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt(s).
��1����PQ��ACʱ����t��ֵ��
��2����tΪ��ֵʱ��QB=QP��
��3����tΪ��ֵʱ����PBQ���������4.8cm 2.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com