
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法如多项式除以多项式可以类比于多位数的除法进行计算:
![]()
![]()
![]()
![]()
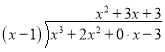
![]()
![]()
![]()
请用以上方法解决下列问题:
(1)计算:![]() ;
;
(2)若关于x的多项式![]() 能被二项式
能被二项式![]() 整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD和正方形BEFG如图(一)所示放置,已知AB=5![]() ,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
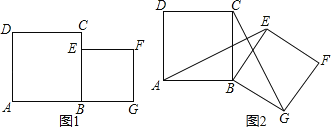
(1)求线段AE与CG的关系,并给出证明
(2)当旋转至某一个角度时,点C,E,G在同一条直线上,请画出示意图形,并求出此时AE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
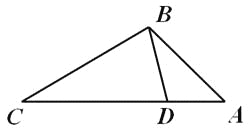
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
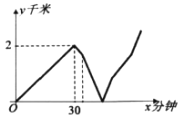
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.

(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() .P是底边
.P是底边![]() 上的一个动点(P与B、C不重合),以P为圆心,
上的一个动点(P与B、C不重合),以P为圆心,![]() 为半径的
为半径的![]() 与射线
与射线![]() 交于点D,射线
交于点D,射线![]() 交射线
交射线![]() 于点E.
于点E.
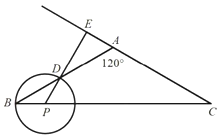
(1)若点E在线段![]() 的延长线上,设
的延长线上,设![]() ,
,![]() 求y关于x的函数关系式,并写出x的取值范围.
求y关于x的函数关系式,并写出x的取值范围.
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
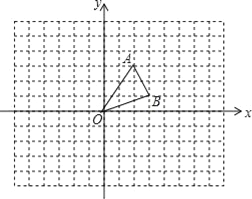
【题目】在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).
(1)将△ABO向左平移4个单位,画出平移后的△A1B1O1.
(2)将△ABO绕点O顺时针旋转180°,画出旋转后得到的△A2B2O.此时四边形ABA2B2的形状是 .
(3)在平面上是否存在点D,使得以A、B、O、D为顶点的四边形是平行四边形,若存在请直接写出符合条件的所有点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(0,2),C(2,1);
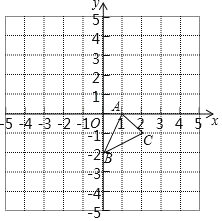
(1)以原点O为位似中心,在第二象限画出△A1B1C1,使△A1B1C1与△ABC的位似比为2:1;
(2)点P(a,b)为线段AC上的任意一点,则点P在△A1B1C1中的对应点P1的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com