
【题目】如图,![]() 中,
中,![]() ,
,![]() .P是底边
.P是底边![]() 上的一个动点(P与B、C不重合),以P为圆心,
上的一个动点(P与B、C不重合),以P为圆心,![]() 为半径的
为半径的![]() 与射线
与射线![]() 交于点D,射线
交于点D,射线![]() 交射线
交射线![]() 于点E.
于点E.
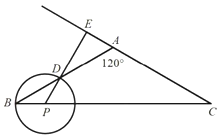
(1)若点E在线段![]() 的延长线上,设
的延长线上,设![]() ,
,![]() 求y关于x的函数关系式,并写出x的取值范围.
求y关于x的函数关系式,并写出x的取值范围.
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】我们定义:如图1、图2、图3,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的![]() 均是
均是![]() 的“旋补三角形”.
的“旋补三角形”.
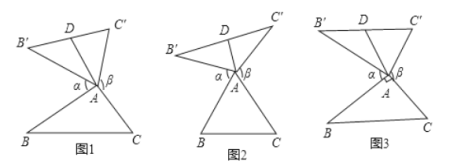
(1)①如图2,当![]() 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”![]() 与
与![]() 的数量关系为:
的数量关系为:![]() ______
______![]() ;
;
②如图3,当![]() ,
,![]() 时,则“旋补中线”
时,则“旋补中线”![]() 长为______.
长为______.
(2)在图1中,当![]() 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法如多项式除以多项式可以类比于多位数的除法进行计算:
![]()
![]()
![]()
![]()
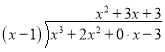
![]()
![]()
![]()
请用以上方法解决下列问题:
(1)计算:![]() ;
;
(2)若关于x的多项式![]() 能被二项式
能被二项式![]() 整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
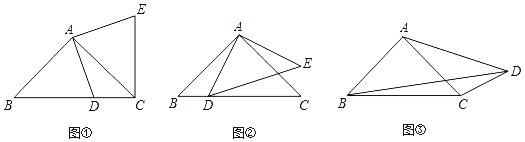
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,P是边BC的中点,PD⊥AB,PE⊥AC,垂足分别为D、E
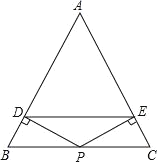
(1)求证:PD=PE;
(2)DE与BC平行吗?请说明理由;
(3)请添加一个条件,使四边形ADPE为正方形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
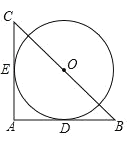
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60,得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB=60;③∠ADE=∠BDC,其中正确结论的序号是( )
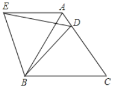
A.①②B.①③C.②③D.只有①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com