
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.

(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
【答案】(1)AB=4;(2)①(![]() ,3);D(-2
,3);D(-2![]() );②D(
);②D(![]() ).
).
【解析】
(1)根据一次函数的解析式求出A,B两点的坐标,再利用勾股定理即可求出AB的长;(2)①连接OM,由OM为Rt△AOB斜边AB上中线,证得△OBM为等边三角形,则∠OBM=60°,得到∠BAO=30°,再分∠DBH=2∠BAO=60°时与∠BDH=2∠BAO=60°时两种情况分别讨论求解;②当∠DBH=45°时,易得∠DAB=45°,则AH=DH=BH,所以M、H重合,作DC⊥y轴于C,DE⊥x轴于E,易证△DCB≌△DEA,得CB=AE,设CB=AE=a,则DC=OE=2![]() ,因为BD=
,因为BD=![]() ,由勾股定理得,DC2+CB2=DB2,所以
,由勾股定理得,DC2+CB2=DB2,所以![]() ,求出a的值,再根据题意舍去一个,即可求解.
,求出a的值,再根据题意舍去一个,即可求解.
解:(1)对于y=![]() ,
,
当x=0时,y=2;当y=0时,x=-2![]() .
.
所以点A(-2![]() ,B(0,2),
,B(0,2),
所以OB=2,OA=2![]() .根据勾股定理得,AB=
.根据勾股定理得,AB=![]() =4.
=4.
(2)①连接OM.
因为OM为Rt△AOB斜边AB上中线,
所以OM=AM=BM=![]() AB=2=OB,
AB=2=OB,
所以△OBM为等边三角形,则∠OBM=60°,
故∠BAO=30°.
1)如图,当∠DBH=2∠BAO=60°时,
连接DM,并延长交AO于点N.
∵∠DBH=60°,DM=BM,
∴△BDM为等边三角形,
∴∠DMB =60°,
故∠AMN=∠DMB =60°,
所以∠MNA=180-30°-60°=90°,
所以MN⊥AO,即DN⊥AO,
∴ON=![]() AO=
AO=![]()
DN=DM+MN=BM+![]() AM=
AM=![]() AB+
AB+![]() AB=3,
AB=3,
所以D(![]() ,3);
,3);
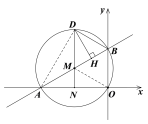
2)如图,
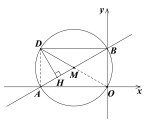
当∠BDH=2∠BAO=60°时,
∵DM=BM=AM=OM,
∴四边形BDAO为矩形,
可得,DA=BO=2,BD=OA=2![]() .
.
所以D(-2![]() ).
).
②如图,
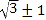
当∠DBH=45°时,
∵AH=BH,DM⊥AB,∴△ABD为等腰直角三角形,
∴∠DAB=45°,
则AH=DH=BH,所以M、H重合.
作DC⊥y轴于C,DE⊥x轴于E,
∵DE⊥AO,DC⊥CO,
∴∠ADE+∠EDB=90°,又∠EDB+∠BDC=90°,
∴∠ADE=∠BDC
又AD=BD,
∴△DCB≌△DEA(AAS),得CB=AE,
设CB=AE=a,则DC=OE=2![]() ,
,
因为BD=![]() ,
,
由勾股定理得,DC2+CB2=DB2,
所以![]() ,
,
解得a=![]() ,
,
当a=![]() 时,OC=DE=3+
时,OC=DE=3+![]() >4,不符合题意.
>4,不符合题意.
当a=![]() 时,OC=OE=
时,OC=OE=![]() ,所以D(
,所以D(![]() )
)


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
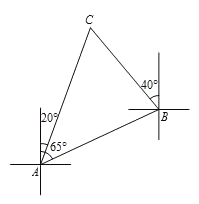
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
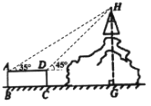
【题目】如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上,在点A处测得塔顶H的仰角为35°,在点D处测得塔顶H的仰角为45°,又测得圆柱形建筑物的上底面直径AD为6m,高CD为2.8m,则塔顶端H到地面的高度HG为( )
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法如多项式除以多项式可以类比于多位数的除法进行计算:
![]()
![]()
![]()
![]()
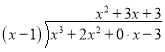
![]()
![]()
![]()
请用以上方法解决下列问题:
(1)计算:![]() ;
;
(2)若关于x的多项式![]() 能被二项式
能被二项式![]() 整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形![]() .点E、F分别在边
.点E、F分别在边![]() 和
和![]() 上,
上,![]() 、
、![]() 和四边形
和四边形![]() 均由单一材料制成,制成
均由单一材料制成,制成![]() 、
、![]() 和四边形
和四边形![]() 的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形
的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形![]() .设
.设![]() .
.
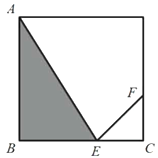
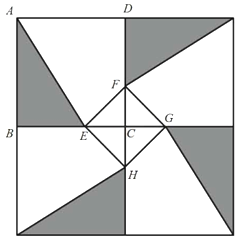
(1)![]() ________,
________,![]() _________.(用含有x的代数式表示).
_________.(用含有x的代数式表示).
(2)已知烧制该种地砖平均每块需加工费0.35元,若要![]() 长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则
长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则![]() 长应为多少米?
长应为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
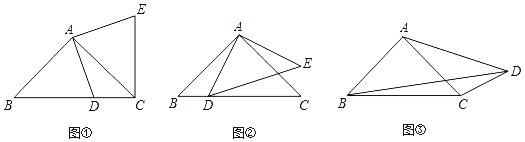
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
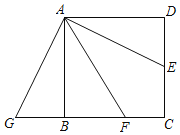
【题目】如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,OB=OC=2,AB=![]() .
.
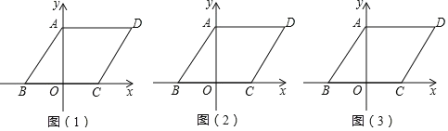
(1)求点D的坐标,直线CD的函数表达式;
(2)已知点P是直线CD上一点,当点P满足S△PAO=![]() S△ABO时,求点P的坐标;
S△ABO时,求点P的坐标;
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F(不与A、B重合),使以A、 C、 F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com