
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,OB=OC=2,AB=![]() .
.
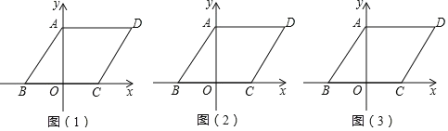
(1)求点D的坐标,直线CD的函数表达式;
(2)已知点P是直线CD上一点,当点P满足S△PAO=![]() S△ABO时,求点P的坐标;
S△ABO时,求点P的坐标;
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F(不与A、B重合),使以A、 C、 F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
【答案】(1)D(4,3),![]() ;(2)P(3,
;(2)P(3,![]() )或(-3,
)或(-3,![]() );(3)F(-3,0)或(2,6)或(
);(3)F(-3,0)或(2,6)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先求出A点坐标,然后根据菱形的性质得到D点的坐标,利用C,D两点的坐标求出解析式;
(2)利用点P是直线CD上一点,AO为△PAO的底边不变,并且S△PAO=![]() S△ABO,分两种情况讨论即可;
S△ABO,分两种情况讨论即可;
(3)根据菱形的性质,分AC、AF是邻边,AC、AF是邻边,AC是对角线,AF是对角线四种的情况分别进行求解计算.
解:∵OB=OC=2,AB=![]() ,
,
∴AD=OB+OC=2+2=4,
![]() ,
,
∴A点的坐标为:(0,3),
D点的坐标为:(4,3),
C点的坐标为:(2,0),
设直线CD的函数表达式为:![]() ,
,
∴将C,D点的坐标代入,得:
![]() ,解之得:
,解之得: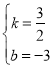 ,
,
∴直线CD的函数表达式为:![]() ,
,
(2)
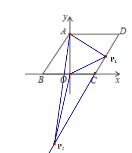
如图示:∵![]()
∴![]()
设P点坐标为(![]() ,
,![]() )
)
即:![]() ,
,
∴![]() ,
,
则:![]() ,或
,或![]()
∴![]() ,或
,或![]()
即P点坐标为(![]() ,
,![]() )或(-3,
)或(-3,![]() );
);
(3) ∵由(1)得OB=OC=2,AB=![]() ,OA=3,
,OA=3,
∴AC=![]() ,
,
①当AC、AF是邻边时,如图示,
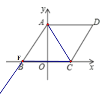
AF=AC=![]() ,即点F与B重合,
,即点F与B重合,
∴F的坐标为(-3,0),
②当AC、AF是邻边,如图示,
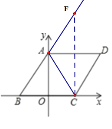
M在直线AD上,且FC垂直平分AM,C,F沿AD成轴对称,
则F的坐标为:(2,6),
③AC是对角线时,如图示:
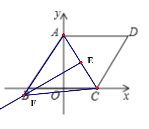
作AC垂直平分线FE,
∵AC经过A(0,3),C(2,0),
∴AC解析式为:![]() ,并且E点的坐标为(1,
,并且E点的坐标为(1,![]() ),
),
∵![]() ,
,
∴设FE的解析式为:![]() ,将E点坐标,代入化简得:
,将E点坐标,代入化简得:
FE的解析式为:![]()
又∵AB经过A(0,3),B(-2,0),
∴AB解析式为:![]() ,
,
∴F点的坐标为方程组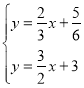 的解,
的解,
解之得: ,
,
∴则F的坐标为:(![]() ,
,![]() ),
),
④AF是对角线时,如图示:
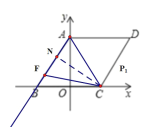
过C作AB垂线,垂足为N,
则![]()
∵![]() ,
,
∴![]() ,
,
∴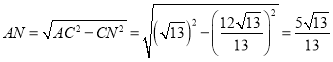 ,
,![]() ,
,
设F点的横坐标为![]() ,根据F点在AB上,并AB解析式为:
,根据F点在AB上,并AB解析式为:![]() ,
,
∴F的坐标为:(![]() ,
,![]() ),
),
则根据勾股定理,有: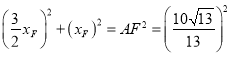
∴![]() ,
,![]() ,
,
∴![]()
∴F的坐标为:(![]() ,
,![]() )
)
综上所述,F点的坐标为:(-3,0)或(2,6)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.

(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
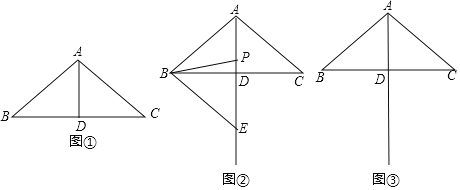
【题目】如图①,在△ABC中,AB=AC=3,∠BAC=100°,D是BC的中点.
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转80°,点B的对应点是点E,连接BE,得到△BPE.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.
请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①∠BEP= °;
②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出△BPE,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(0,2),C(2,1);
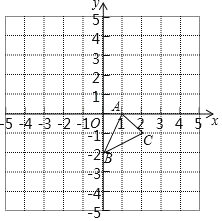
(1)以原点O为位似中心,在第二象限画出△A1B1C1,使△A1B1C1与△ABC的位似比为2:1;
(2)点P(a,b)为线段AC上的任意一点,则点P在△A1B1C1中的对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=40°,则∠ACB=( ).
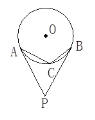
A.70°B.80°C.110°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
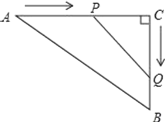
【题目】如图,在△ABC中,AB=10![]() m,BC=40m,∠C=90°,点P从点A开始沿边AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动,几秒时,△PCQ的面积等于432m2?
m,BC=40m,∠C=90°,点P从点A开始沿边AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动,几秒时,△PCQ的面积等于432m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
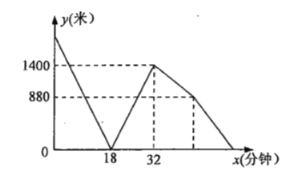
【题目】甲,乙两人分别从![]() ,
,![]() 两地相向而行,甲先走3分钟后乙才开始行走,甲到达
两地相向而行,甲先走3分钟后乙才开始行走,甲到达![]() 地后立即停止,乙到达
地后立即停止,乙到达![]() 地后立即以另一速度返回
地后立即以另一速度返回![]() 地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离
地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离![]() (米)与乙出发的时间
(米)与乙出发的时间![]() (分钟)的函数关系如图所示.当甲到达
(分钟)的函数关系如图所示.当甲到达![]() 地时,则乙距离
地时,则乙距离![]() 地的时间还需要________分钟.
地的时间还需要________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
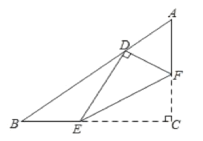
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com