【题目】甲，乙两人分别从
，
两地相向而行，甲先走3分钟后乙才开始行走，甲到达地后立即停止，乙到达地后立即以另一速度返回地，在整个行驶的过程中，两人保持各自速度匀速行走，甲，乙两人之间的距离
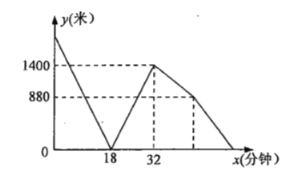
（米）与乙出发的时间
（分钟）的函数关系如图所示.当甲到达地时，则乙距离地的时间还需要________分钟.
【答案】11
【解析】
在乙出发后18分钟两车相遇，两车相遇后，又经过32-18=14分钟，两车之间的距离达到最大1400米，可以求出两车的速度和为：1400÷（32-18）=100米/分，说明此时乙车已到A地，于是可以得到：甲从开始到第一次相遇地点用时3+18=21分，而乙用14分，因此甲的速度是乙的
，根据速度和是100米/分，可求出乙车的速度为60米/分，甲车速度为40米/分；AB两地的路程为：60×32=1920米，当乙到A地时，甲距B地还有1920-1400=520米，因此甲到B地需要520÷40=13分，乙以另一速度返回13秒走的路程1920-880=1040米，所以返回速度为1040÷13=80米，到B地还要880÷80=11分．
解：两车的速度和为：1400÷（32-18）=100米/分，
甲从开始到第一次相遇地点用时3+18=21分，而乙相遇后只用14分，因此甲的速度是乙的，
甲速度为100×
=40米/分，乙的速度为100×
=60米/分，
∴AB两地的路程为：60×32=1920米，
当乙到A地时，甲距B地还有1920-1400=520米，
因此甲到B地需要520÷40=13分，
乙以另一速度返回13秒走的路程1920-880=1040米，
所以返回速度为1040÷13=80米，
到B地还要880÷80=11分．
故答案为：11
阅读快车系列答案科目：初中数学 来源： 题型：
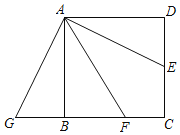
【题目】如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，四边形ABCD是平行四边形，OB=OC=2，AB=
.
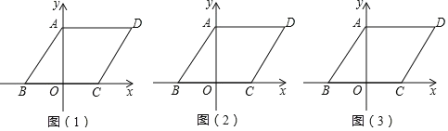
(1)求点D的坐标，直线CD的函数表达式；
(2)已知点P是直线CD上一点，当点P满足S△PAO=
S△ABO时，求点P的坐标；
(3)若点M在平面直角坐标系内，则在直线AB上是否存在点F（不与A、B重合），使以A、 C、 F、M为顶点的四边形为菱形?若存在，直接写出F点的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(9分)已知：
ABCD的两边AB，AD的长是关于x的方程
的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么ABCD的周长是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一、阅读材料：
已知实数m，n满足（2m2＋n2＋1）（2m2＋n2－1）=80，试求2m2＋n2的值．
解：设2m2＋n2=t，则原方程变为（t＋1）（t－1）=80，整理得t2－1=80，t2=81，所以t=土9，因为2m2＋n2＞0，所以2m2＋n2=9．
二、方法归纳：
上面这种方法称为“ 法”，把其中某些部分看成一个整体，并用新字母代替（即换元），则能使复杂的问题简单化．
三、探索实践：
根据以上阅读材料内容，解决下列问题，并写出解答过程．
（1）已知实数x、y，满足（2x2＋2y2＋3）（2x2＋2y2－3）=27，求x2＋y2的值．
（2）已知Rt△ACB的三边为a、b、c（c为斜边），其中a、b满足（a2＋b2）（a2＋b2－4）=5，求Rt△ACB外接圆的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】闺蜜装在大学校园里盛行，闺蜜装能很好的表达“亲如姐妹”的友谊，也能成为校园一道靓丽的风景.某专卖店购进一批
，
两款闺蜜装，共花费了18400元，款比款多20套，其中每套款闺蜜装进价200元，每套款闺蜜装进价160元.进行试销售，供不应求，很快销售完毕，己知每套款闺蜜装售价为240元.
（1）求购进，两款闺蜜装各多少套？
（2）国庆将至，专卖店又购进第二批，两款闺蜜装并进行促销活动，在促销期间，每套款闺蜜装在进价的基础上提高
销售，每套款闺蜜装在第一批售价的基础上降低
销售，结果在促销售活动中，款闺蜜装的销量比第一批款销售量降低了
，款闺蜜装的销售量比第一批款销售量上升了
，结果本次促销活动共获利5200元，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】）甲乙两人在相同条件下完成了5次射击训练，两人的成绩如图所示．
（1）甲射击成绩的众数为 环，乙射击成绩的中位数为 环；
（2）计算两人射击成绩的方差；
（3）根据训练成绩，你认为选派哪一名队员参赛更好，为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
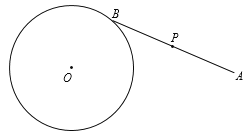
【题目】如图，⊙O的半径为2，O到定点A的距离为5，点B在⊙O上，点P是线段AB的中点．若B在⊙O上运动一周：
（1）证明点P运动的路径是一个圆．
（思路引导：要证点P运动的路径是一个圆，只要证点P到定点M的距离等于定长r，由图中的定点、定长可以发现M、r．）
（2）△ABC始终是一个等边三角形，直接写出PC长的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
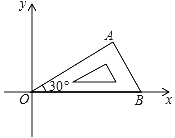
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中，OB 在 x轴上，若 OA＝2，将三角板绕原点 O 顺时针旋转 75°，则点 A 的对应点 A′ 的坐标为___________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com