
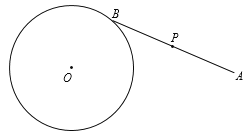
【题目】如图,⊙O的半径为2,O到定点A的距离为5,点B在⊙O上,点P是线段AB的中点.若B在⊙O上运动一周:
(1)证明点P运动的路径是一个圆.
(思路引导:要证点P运动的路径是一个圆,只要证点P到定点M的距离等于定长r,由图中的定点、定长可以发现M、r.)
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
【答案】(1)见解析 (2)![]() ≤PC≤
≤PC≤![]()
【解析】
(1)连接OA、OB,取OA的中点H,连接OB,HP,则HP是△ABO的中位线,HP=![]() OB=1,即可得出结论;
OB=1,即可得出结论;
(2)连接AO并延长AO交⊙O于点M、N,由等边三角形的性质得出PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,得出PC=
BC,得出PC=![]() AB,分别求出PC的最小值和最大值,即可得出答案.
AB,分别求出PC的最小值和最大值,即可得出答案.
(1)证明:连接OA、OB,取OA的中点H,连接OB,HP,如图1所示:
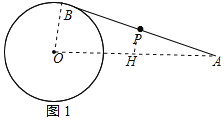
则HP是△ABO的中位线,HP=![]() OB=1,
OB=1,
∵点O与点A是定点,
∴OA的中点H也是定点,
∴B在⊙O上运动,
则点P随之运动,但HP=![]() OB=1不变,
OB=1不变,
∴B在⊙O上运动一周,点P运动的路径是以点H为圆心,半径为1的一个圆;
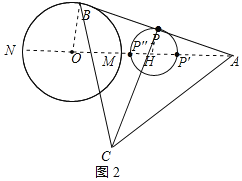
(2)解:连接AO并延长AO交⊙O于点M、N,如图2所示:
∵△ABC是等边三角形,点P是线段AB的中点,
∴PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,
BC,
∴PC=![]() AB,
AB,
当点B运动到点M位置时,点P运动到点P'位置,PC最短,
∵AM=OA-OM=5-2=3,
∴AP'=![]() AM=
AM=![]() ,
,
∴PC=![]() ;
;
当点B运动到点N位置时,点P运动到点P'位置,PC最长,
∵AN=OA+ON=5+2=7,
∴AP'=![]() ,
,
∴PC=![]() ;
;
∴PC长的取值范围是![]() ≤PC≤
≤PC≤![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人分别从![]() ,
,![]() 两地相向而行,甲先走3分钟后乙才开始行走,甲到达
两地相向而行,甲先走3分钟后乙才开始行走,甲到达![]() 地后立即停止,乙到达
地后立即停止,乙到达![]() 地后立即以另一速度返回
地后立即以另一速度返回![]() 地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离
地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离![]() (米)与乙出发的时间
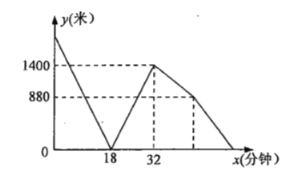
(米)与乙出发的时间![]() (分钟)的函数关系如图所示.当甲到达
(分钟)的函数关系如图所示.当甲到达![]() 地时,则乙距离
地时,则乙距离![]() 地的时间还需要________分钟.
地的时间还需要________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
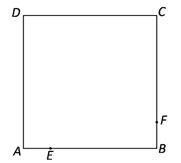
【题目】如图,已知正方形ABCD的边长为4 cm,点E从点A出发,以1cm/s的速度沿着折线A→B→C运动,到达点C时停止运动;点F从点B出发,也以1cm/s的速度沿着折线B→C→D运动,到达点D时停止运动.点E、F分别从点A、B同时出发,设运动时间为t(s).
(1)当t为何值时,E、F两点间的距离为2![]() cm;
cm;
(2)连接DE、AF交于点M,
①在整个运动过程中,CM的最小值为 cm;
②当CM=4 cm时,此时t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( )
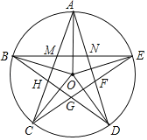
A.① ②B.① ③C.② ③D.① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
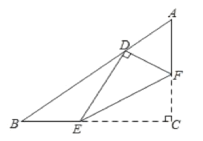
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
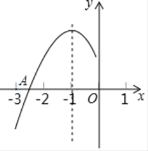
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
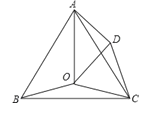
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=4,OC=5,求AO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com