
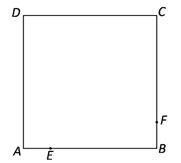
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4 cm����E�ӵ�A��������1cm/s���ٶ���������A��B��C�˶��������Cʱֹͣ�˶�����F�ӵ�B������Ҳ��1cm/s���ٶ���������B��C��D�˶��������Dʱֹͣ�˶�����E��F�ֱ�ӵ�A��Bͬʱ���������˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ��E��F�����ľ���Ϊ2![]() cm��
cm��
��2������DE��AF���ڵ�M��
���������˶������У�CM����СֵΪ cm��
�ڵ�CM��4 cmʱ����ʱt��ֵΪ .
���𰸡���1��t1��2+![]() ��t2��2��
��t2��2��![]() �� t3��6+
�� t3��6+![]() ��t4��6��
��t4��6��![]() . ��2���� 2
. ��2���� 2![]() ��2���� 2��8.
��2���� 2��8.
��������
��1�����������ȷ��E,F��λ�ã����ݹ��ɶ�����ֵ��
��2���ٸ��������������M���˶��켣��Բ��Ȼ���������֮���߶����ȷ����Сֵ��
����֤��DAM�ա�CDN����DAE�ס�DMA��������������.
��1�� �⣺��E��F����ֱ���AB��BC��ʱ��
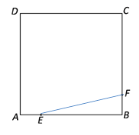
��AE= t��EB=4��t��BF= t
��EB2��BF2��EF2
��t2����4��t��2��(2![]() )2
)2
�� t1��2+![]() ��t2��2��
��t2��2��![]() .
.
��E��F����ֱ���BC��CD��ʱ��
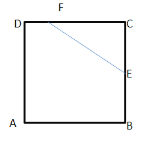
��CE=8��t��EB=t��4
��CE2��CF2��EF2
��(8��t)2����t��4��2��(2![]() )2
)2
�� t1��6+![]() ��t2��6��
��t2��6��![]() .
.
��2��
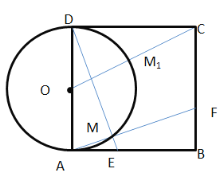
��E,F�����ٶ���ͬ����AE=BF
�֡�������ABCD�У�AD=BA,��DAB=��B=90�㣬
���DAE�ա�ABF��
���ADE=��BAF
���ADE+DAF=90�㣬����AMD=90��
���Ե�M����OΪԲ�ģ�ADΪֱ����Բ�ϣ�����OC��ԲO�ڵ�M1,��ʱCM������̣���Rt��DOC�У�CO=![]()
����CM����СֵΪ![]() cm��
cm��
��
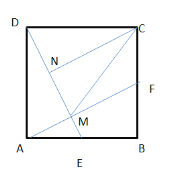
��ͼ������C��CN��DE����������֤����DAM�ա�CDN����DN=AM���֡�CM=CD=4,��CN��DE����DM=2AM,��![]()
����һ�ʿ�֪����AMD=90�㣬���DAE=��AMD,��ADM=��EDA
���DAE�ס�DMA
��![]()
��t=AE=2��
����E�����C,��F�����D����ʱAM=4����ʱt=8,
���ϣ���CM��4 cmʱ����ʱt��ֵΪ2��8.


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C����ABC��BE��AC������Ϊ��E����BDE�ǵȱ������Σ���AD��4�����߶�BE�ij�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(9��)��֪��![]() ABCD������AB��AD�ij��ǹ���x�ķ���
ABCD������AB��AD�ij��ǹ���x�ķ���![]() ������ʵ������
������ʵ������
��1����mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ô![]() ABCD���ܳ��Ƕ��٣�
ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ�ڴ�ѧУ��ʢ�У�����װ�ܺܺõı�������������������꣬Ҳ�ܳ�ΪУһ�������ķ羰.ijר���깺��һ��![]() ��
��![]() �������װ����������18400Ԫ��
�������װ����������18400Ԫ��![]() ���
���![]() ���20�ף�����ÿ��
���20�ף�����ÿ��![]() �����װ����200Ԫ��ÿ��
�����װ����200Ԫ��ÿ��![]() �����װ����160Ԫ.���������ۣ�����Ӧ�ܿ�������ϣ���֪ÿ��
�����װ����160Ԫ.���������ۣ�����Ӧ�ܿ�������ϣ���֪ÿ��![]() �����װ�ۼ�Ϊ240Ԫ.
�����װ�ۼ�Ϊ240Ԫ.
��1����![]() ��
��![]() �������װ�������ף�
�������װ�������ף�
��2�����콫����ר�����ֹ����ڶ���![]() ��
��![]() �������װ�����д�������ڴ����ڼ䣬ÿ��
�������װ�����д�������ڴ����ڼ䣬ÿ��![]() �����װ�ڽ��۵Ļ��������
�����װ�ڽ��۵Ļ��������![]() ���ۣ�ÿ��
���ۣ�ÿ��![]() �����װ�ڵ�һ���ۼ۵Ļ����Ͻ���
�����װ�ڵ�һ���ۼ۵Ļ����Ͻ���![]() ���ۣ�����ڴ����ۻ�У�
���ۣ�����ڴ����ۻ�У�![]() �����װ�������ȵ�һ��
�����װ�������ȵ�һ��![]() ��������������
��������������![]() ��
��![]() �����װ���������ȵ�һ��
�����װ���������ȵ�һ��![]() ��������������
��������������![]() ��������δ����������5200Ԫ����
��������δ����������5200Ԫ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ͬ�����������5�����ѵ�������˵ijɼ���ͼ��ʾ��

��1��������ɼ�������Ϊ ����������ɼ�����λ��Ϊ ����
��2��������������ɼ��ķ��
��3������ѵ���ɼ�������Ϊѡ����һ����Ա�������ã�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��
��1��x2+1��3x
��2����x��2����x��3����12
��3����2x��3��2+x��2x��3����0����ʽ�ֽⷨ��
��4��2x2��4x��1��0�����䷽������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
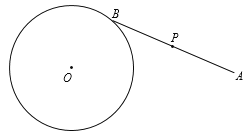
����Ŀ����ͼ����O�İ뾶Ϊ2��O������A�ľ���Ϊ5����B�ڡ�O�ϣ���P���߶�AB���е㣮��B�ڡ�O���˶�һ�ܣ�
��1��֤����P�˶���·����һ��Բ��
��˼·������Ҫ֤��P�˶���·����һ��Բ��ֻҪ֤��P������M�ľ�����ڶ���r����ͼ�еĶ��㡢�������Է���M��r����
��2����ABCʼ����һ���ȱ������Σ�ֱ��д��PC����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������壩�������Σ����ǵ��������Σ�һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
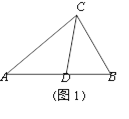
��1����ͼ1����ABC�У���A��40������B��60����CDƽ�֡�ACB����֤��CDΪ��ABC�������ָ��ߣ�
��2���ڡ�ABC�У�CD�ǡ�ABC�������ָ��ߣ����С�ACDΪ���������Σ����A��x������B��y������y��x֮��Ĺ�ϵʽΪ_____________________________��
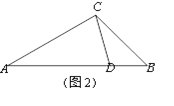
��3����ͼ2����ABC�У�AC��2��BC��![]() ��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��8mʱ��ˮ���ABΪ12m����ˮ������6mʱ�ﵽ����ˮλ����ʱ�����ڵ�ˮ������Ƕ���m��
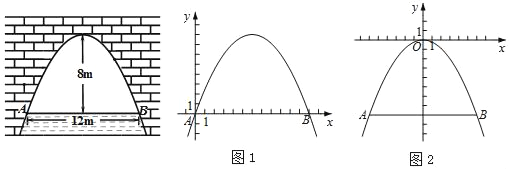
��������˽�������������ַ������벹��������
����һ����ͼ1���Ե�AΪԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��B������Ϊ���� ������ �����������ߵĶ�������Ϊ���� ������ ������
������������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y��6ʱ�������ʱ�Ա���x��ȡֵ�����ɽ��������⣮
����������ͼ2���������߶���Ϊԭ�㣬�Գ���Ϊy�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y���� ��ʱ�������ʱ�Ա���x��ȡֵΪ�� �������ɽ��������⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com