
【题目】(定义)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
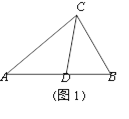
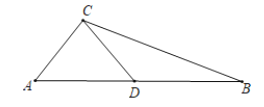
(1)如图1,△ABC中,∠A=40°,∠B=60°,CD平分∠ACB.求证:CD为△ABC的完美分割线;
(2)在△ABC中,CD是△ABC的完美分割线,其中△ACD为等腰三角形,设∠A=x°,∠B=y°,则y与x之间的关系式为_____________________________;
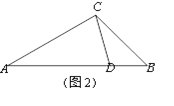
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
【答案】(1)详见解析;(2)3x+y=180或3x+2y=180;(3)CD=![]()
【解析】
(1)据完美分割线①△ABC不是等腰三角形,②△ACD等三角形,③△BDC∽△BCA即可
(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出x,y的关系即可.
(3)由题意可知,AC=AD=2;然后运用相似三角形的性质和判定以及勾股定理求解即可.
(1)证明:∵ ∠A=40°,∠B=60°
∴∠ACB=80°
∴△ABC不是等腰三角形
∵CD平分∠ACB
∴∠ACD=∠DCB=40°
∴△ACD是等腰三角形
∵∠A=∠DCB=40° ∠B=∠B
∴ △BCD∽△BAC
∴CD为△ABC的完美分割线
(2)①当AD=CD时,如图
∴∠ACD=∠A=x
∴∠CDA=∠ACD+∠A=2x
又∵△BCD∽△BAC
∴∠DCB=∠A=x
∴x+2x+y=180°,即3x+y=180
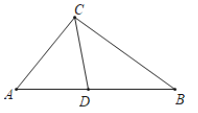
②当AD=AC时,如图
∴![]()
又∵△BCD∽△BAC
∴∠DCB=∠A=x
∴x+y=![]() ,即3x+2y=180°
,即3x+2y=180°
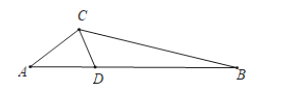
③当AD=AC时,如图![]()
![]()
![]() ,矛盾,舍弃.
,矛盾,舍弃.
故y与x之间的关系式为3x+y=180或3x+2y=180
(3)由题意得AC=AD=2
∵△BCD∽△BAC
∴![]() =
= ![]() 设BD=x
设BD=x
则x(x+2)=(![]() )2
)2
解得x1=1 x2=-3(舍去)
∴ BD=1
∵△BCD∽△BAC
∴![]() =
= ![]() 即
即![]() =
= ![]()
∴CD=![]()


科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=40°,则∠ACB=( ).
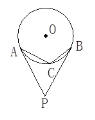
A.70°B.80°C.110°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
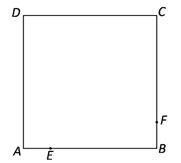
【题目】如图,已知正方形ABCD的边长为4 cm,点E从点A出发,以1cm/s的速度沿着折线A→B→C运动,到达点C时停止运动;点F从点B出发,也以1cm/s的速度沿着折线B→C→D运动,到达点D时停止运动.点E、F分别从点A、B同时出发,设运动时间为t(s).
(1)当t为何值时,E、F两点间的距离为2![]() cm;
cm;
(2)连接DE、AF交于点M,
①在整个运动过程中,CM的最小值为 cm;
②当CM=4 cm时,此时t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( )
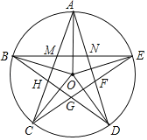
A.① ②B.① ③C.② ③D.① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
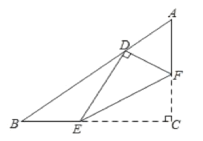
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交![]() 轴于点B、C.解答下列问题:
轴于点B、C.解答下列问题:
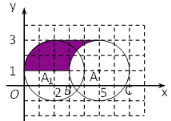
(1)将⊙A向下平移 个单位长度与![]() 轴相切;
轴相切;
(2) 将⊙A向左平移得到⊙A1,当⊙A1与![]() 轴首次相切,此时阴影部分的面积S= ;
轴首次相切,此时阴影部分的面积S= ;
(3)将⊙A向左平移 个单位长度与坐标轴有三个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
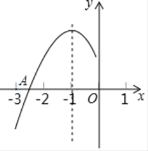
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
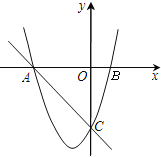
【题目】如图,二次函数![]() 的图象与x轴交于A、B 两点,与y轴交于点C,且点B的坐标为(1,0),点C的坐标为(0,﹣3),一次函数y2=mx+n的图象过点A、C.
的图象与x轴交于A、B 两点,与y轴交于点C,且点B的坐标为(1,0),点C的坐标为(0,﹣3),一次函数y2=mx+n的图象过点A、C.
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的另一个交点A的坐标;
(3)根据图象写出y2<y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com