
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交![]() 轴于点B、C.解答下列问题:
轴于点B、C.解答下列问题:
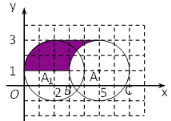
(1)将⊙A向下平移 个单位长度与![]() 轴相切;
轴相切;
(2) 将⊙A向左平移得到⊙A1,当⊙A1与![]() 轴首次相切,此时阴影部分的面积S= ;
轴首次相切,此时阴影部分的面积S= ;
(3)将⊙A向左平移 个单位长度与坐标轴有三个公共点.
【答案】(1)3;(2)6;(3)3,![]() ,
,![]() ,7.
,7.
【解析】
(1)根据直角坐标系与相切的性质即可得到平移的距离;
(2)根据直线和圆相切的位置关系与数量之间的联系,得到A点坐标,再跟平移的性质即可求出阴影部分面积;
(3)由⊙A已经与x轴交于两点,故分圆与y轴相切与或圆过原点两种情况进行求解即可.
将⊙A向下平移3个单位长度与![]() 轴相切,
轴相切,
故填:3.
(2)根据直线和圆相切的位置关系与数量之间的联系,得点A′的坐标是(2,1);
则移动的距离是52=3;
根据平移变换的性质,则阴影部分的面积为3×2=6
故填:6;
(3)∵⊙A已经与x轴交于两点,
∴①圆与y轴相切
由圆心A的坐标为(5,1),2个单位长度为半径
故向左平移3或7个单位长度可与y轴相切;
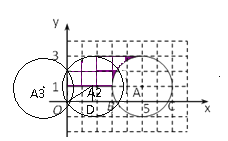
②圆过原点时,如图⊙A2,作A2D⊥x轴于D点,连接A2O,
故OD=![]()
此向左平移5-![]() 个单位长度,
个单位长度,
同理可得平移至⊙A3时,平移距离为![]()
综上故填:3,![]() ,
,![]() ,7.
,7.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
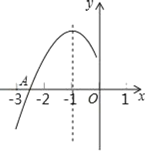
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0和(﹣2,0)之间,其部分图象如图,则下列结论:①2a﹣b=0:②4ac﹣b2<0:③点(x1,y1),(x2,y2)在抛物线上若x1<x2,则y1<y2;④a+b+c<0.正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的两个交点间的距离为2.
轴的两个交点间的距离为2.
(1)若此抛物线的对称轴为直线![]() ,请判断点(3,3)是否在此抛物线上?
,请判断点(3,3)是否在此抛物线上?
(2)若此抛物线的顶点为(S,t),请证明![]() ;
;
(3)当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
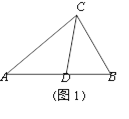
(1)如图1,△ABC中,∠A=40°,∠B=60°,CD平分∠ACB.求证:CD为△ABC的完美分割线;
(2)在△ABC中,CD是△ABC的完美分割线,其中△ACD为等腰三角形,设∠A=x°,∠B=y°,则y与x之间的关系式为_____________________________;
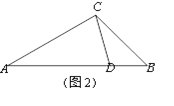
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△OAB,△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)若O、C、A在一条直线上,连AD、BC,分别取AD、BC的中点M、N如图(1),求出线段MN、AC之间的数量关系;
(2)若将△OCD绕O旋转到如图(2)的位置,连AD、BC,取BC的中点M,请探究线段OM、AD之间的关系,并证明你的结论;
(3)若将△OCD由图(1)的位置绕O顺时针旋转角度α(0°<α<360°),且OA=4,OC=2,是否存在角度α使得OC⊥BC?若存在,请直接写出此时△ABC的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
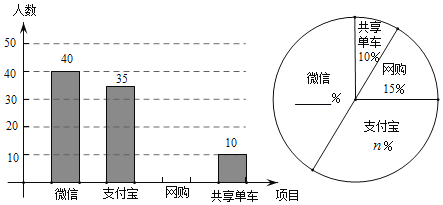
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )
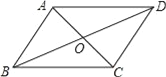
A.AB=ADB.AC⊥BDC.AC=BDD.AD=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利500元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价10元,商场每天可多售出2件.设每件商品降价x元(x是10的整数倍),据此信息,请回答:
(1)商场日销量增加 件,每件商品盈利 元;(用含x的代数式表示).
(2)在上述条件不变且销售正常的情况下,每件商品降价多少元时,商场日盈利可达到21000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com