
【题目】商场某种商品平均每天可销售30件,每件盈利500元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价10元,商场每天可多售出2件.设每件商品降价x元(x是10的整数倍),据此信息,请回答:
(1)商场日销量增加 件,每件商品盈利 元;(用含x的代数式表示).
(2)在上述条件不变且销售正常的情况下,每件商品降价多少元时,商场日盈利可达到21000元?
【答案】(1)![]() ,(500﹣x);(2)每件商品降价200元,商场日盈利可达21000元.
,(500﹣x);(2)每件商品降价200元,商场日盈利可达21000元.
【解析】
(1)由于降价10元,可多售出2件,降价x元,可多售出![]() 件,每件盈利的钱数为500-x;
件,每件盈利的钱数为500-x;
(2)根据等量关系为:每件商品的盈利×可卖出商品的件数=21000,把相关数值代入计算得到合适的解即可.
(1)由题意,可得商场日销量增加![]() 件,每件商品盈利(500﹣x)元;
件,每件商品盈利(500﹣x)元;
故答案为:![]() ,(500﹣x);
,(500﹣x);
(2)由题意得:(500﹣x)(30+![]() )=21000,
)=21000,
化简得:x2﹣350x+30000=0,
即(x﹣150)(x﹣200)=0
解得:x1=150,x2=200,
∵为了尽快减少库存,
∴x=200,
答:每件商品降价200元,商场日盈利可达21000元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交![]() 轴于点B、C.解答下列问题:
轴于点B、C.解答下列问题:
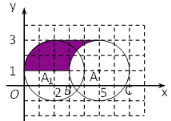
(1)将⊙A向下平移 个单位长度与![]() 轴相切;
轴相切;
(2) 将⊙A向左平移得到⊙A1,当⊙A1与![]() 轴首次相切,此时阴影部分的面积S= ;
轴首次相切,此时阴影部分的面积S= ;
(3)将⊙A向左平移 个单位长度与坐标轴有三个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.当销售单价为多少时,超市每天销售这种玩具可获利润2250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动.
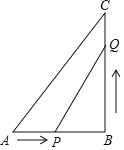
(1)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的面积等于
的面积等于![]() ?
?
(2)如果![]() 分别从
分别从![]() 同时出发,
同时出发,![]() 的面积能否等于
的面积能否等于![]() ?
?
(3)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的长度等于
的长度等于![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
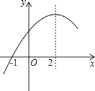
【题目】二次函数![]() 的部分图象如图所示,图象过点(
的部分图象如图所示,图象过点(![]() ,
,![]() ),对称轴为直线
),对称轴为直线![]() ,下列结论:(1)
,下列结论:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)若点
;(4)若点![]() (
(![]() ,
,![]() ),点
),点![]() (
(![]() ,
,![]() ),点
),点![]() (
(![]() ,
,![]() )在该函数图象上,则
)在该函数图象上,则![]() ,其中正确的结论有( )
,其中正确的结论有( )
A.1个B.2C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
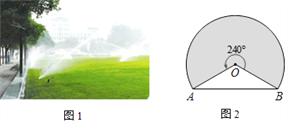
查看答案和解析>>
科目:初中数学 来源: 题型:
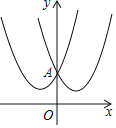
【题目】如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2﹣2x+2是“关于y轴对称二次函数”.
(1)直接写出两条图中“关于y轴对称二次函数”图象所具有的共同特点.
(2)二次函数y=2(x+2)2+1的“关于y轴对称二次函数”解析式为 ;二次函数y=a(x﹣h)2+k的“关于y轴对称二次函数”解析式为 ;
(3)平面直角坐标系中,记“关于y轴对称二次函数”的图象与y轴的交点为A,它们的两个顶点分别为B,C,且BC=6,顺次连接点A,B,O,C得到一个面积为24的菱形,求“关于y轴对称二次函数”的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com