
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动.
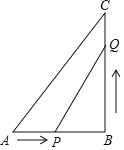
(1)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的面积等于
的面积等于![]() ?
?
(2)如果![]() 分别从
分别从![]() 同时出发,
同时出发,![]() 的面积能否等于
的面积能否等于![]() ?
?
(3)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的长度等于
的长度等于![]() ?
?
【答案】(1)![]() 后,
后,![]() 的面积等于
的面积等于![]() ;(2)
;(2)![]() 的面积不能等于
的面积不能等于![]() .理由见解析;(3)
.理由见解析;(3)![]() 后,
后,![]() 的长度等于
的长度等于![]() .
.
【解析】
(1)设经过x秒钟,△PBQ的面积等于4平方厘米,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;
(2)设经过x秒钟,△PBQ的面积等于4平方厘米,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;
(3)设经过x秒,点P,Q之间的距离为5cm,根据勾股定理列式求解即可;
设![]() 后,
后,![]() ,
,![]() .
.
(1)根据三角形的面积公式列方程,
得:![]() .
.
解得:![]() ,
,![]() .
.
当![]() 时,
时,![]()
![]() ,不合题意,舍去.
,不合题意,舍去.
所以![]() 后,
后,![]() 的面积等于
的面积等于![]()
(2)![]() 的面积不能等于
的面积不能等于![]() .
.
理由:根据三角形的面积公式列方程,
得:![]() ,
,
整理,得:![]() .
.
因为![]() ,
,
所以![]() 的面积不能等于
的面积不能等于![]() .
.
(3)根据勾股定理列方程,
得:![]() .
.
解得:![]() ,
,![]() (不符合题意,舍去).
(不符合题意,舍去).
所以![]() 后,
后,![]() 的长度等于
的长度等于![]()


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在△OAB,△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)若O、C、A在一条直线上,连AD、BC,分别取AD、BC的中点M、N如图(1),求出线段MN、AC之间的数量关系;
(2)若将△OCD绕O旋转到如图(2)的位置,连AD、BC,取BC的中点M,请探究线段OM、AD之间的关系,并证明你的结论;
(3)若将△OCD由图(1)的位置绕O顺时针旋转角度α(0°<α<360°),且OA=4,OC=2,是否存在角度α使得OC⊥BC?若存在,请直接写出此时△ABC的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上,![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.

(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]()
![]() 满足等量关系时,
满足等量关系时,![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中,![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
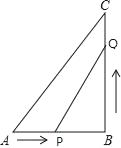
【题目】已知:如图所示.在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于7cm2?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利500元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价10元,商场每天可多售出2件.设每件商品降价x元(x是10的整数倍),据此信息,请回答:
(1)商场日销量增加 件,每件商品盈利 元;(用含x的代数式表示).
(2)在上述条件不变且销售正常的情况下,每件商品降价多少元时,商场日盈利可达到21000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
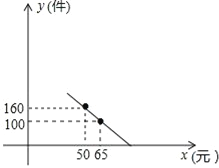
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
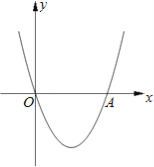
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=![]() ,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转
,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转![]() 角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
小宇发现点E的位置,![]() 和
和![]() 的大小都不确定,于是他从特殊情况开始进行探究.
的大小都不确定,于是他从特殊情况开始进行探究.
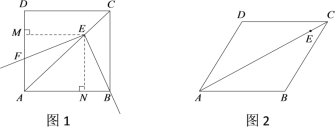
(1)如图1,当![]() =
=![]() =90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得
=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得![]() ,并由全等三角形的性质得到EB与EF的数量关系为 .
,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当![]() =60°,
=60°,![]() =120°时,
=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=![]() ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角
,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角![]() ,
,![]() ,
,![]() 满足的关系: .
满足的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 从
从![]() 处开始按顺时针方向旋转,
处开始按顺时针方向旋转,![]() 交边
交边![]() (或
(或![]() )于点
)于点![]() ,
,![]() 交边
交边![]() (或
(或![]() )于点
)于点![]() ,当
,当![]() 旋转至
旋转至![]() 处时,
处时,![]() 停止旋转.
停止旋转.
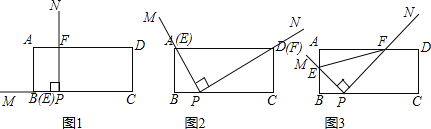
(1)特殊情形:如图2,发现当![]() 过点
过点![]() 时,PN也恰巧过点
时,PN也恰巧过点![]() ,此时
,此时![]()
![]() (填“≌”或“∽”);
(填“≌”或“∽”);
(2)类比探究:如图3,在旋转过程中,![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com