
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上,![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.

(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]()
![]() 满足等量关系时,
满足等量关系时,![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中,![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
【答案】(1)SAS,△AFE;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFG≌△AFE进而得到EF=FG,即可得EF=BE+DF;
(2)∠B+∠D=180°时,EF=BE+DF,与(1)的证法类同;
(3)根据△AEC绕点A顺时针旋转90°得到△ABE′,根据旋转的性质,可知△AEC≌△ABE′得到BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据Rt△ABC中的,AB=AC得到∠E′BD=90°,所以E′B2+BD2=E′D2,证△AE′D≌△AED,利用DE=DE′得到DE2=BD2+EC2;
(1)∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,在△AFE和△AFG中,
∵AE=AG,∠EAF=∠FAG,AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=FG,即:EF=BE+DF.
(2)∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
∵AE=AG,∠FAE=∠FAG,AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=FG,即:EF=BE+DF.

(3)猜想:DE2=BD2+EC2,理由如下:
根据ΔABD绕点A逆时针旋转90°得到ΔACD′,如图,连接ED′.

∴ΔABDΔACD′.
∴CD′=BD,AD′=AD,∠B=∠ACD′,∠BAD=∠D′ AC.
在RtΔABC中,∵AB=AC,
∴∠ABC=∠ACB=45°.
∴∠ACB+∠ACD′=90°,即∠D′ CE=90°,
∴D’C2+CE2=D′E2.
又∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∴∠D′AC+∠EAC=45°,即∠D′ AE=45°.
∴ΔAD′ EΔADE,
∴ED=ED′,
∴DE2=BD2+EC2.


科目:初中数学 来源: 题型:
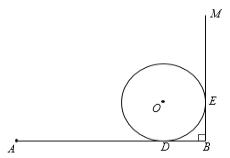
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 ( )
 .
.
A.(-4,3)B.(-3,4)C.(3,-4)D.(4,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是半圆O上的一点,AB是⊙O的直径,D是![]() 的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
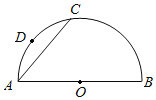
下面是小明的做法,请帮他补充完整(包括补全图形)
解:补全半圆O为完整的⊙O,连接AD,延长DE交⊙O于点H(补全图形)
∵D是![]() 的中点,
的中点,
∴![]() .
.
∵DE⊥AB,AB是⊙O的直径,
∴![]() ( )(填推理依据)
( )(填推理依据)
∴![]()
∴∠ADF=∠FAD( )(填推理依据)
∴AF=DF( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.当销售单价为多少时,超市每天销售这种玩具可获利润2250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动.
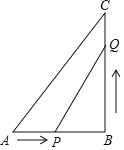
(1)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的面积等于
的面积等于![]() ?
?
(2)如果![]() 分别从
分别从![]() 同时出发,
同时出发,![]() 的面积能否等于
的面积能否等于![]() ?
?
(3)如果![]() 分别从
分别从![]() 同时出发,那么几秒后,
同时出发,那么几秒后,![]() 的长度等于
的长度等于![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com