
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
【答案】(1)见解析;(2)t的值为2-2![]() ≤t≤2+2
≤t≤2+2![]() ;(3)k的值为-3+
;(3)k的值为-3+![]() 或1-
或1-![]() .
.
【解析】
(1)如图1中,作OH⊥AB于H.求出OH即可解决问题.
(2)如图2中,作TH⊥AB于H,交⊙T于D.分两种情形求出d(⊙T,直线AB)=1时,点T的坐标即可.
(3)当直线经过点D(2-![]() ,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-
,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-![]() ,求出直线y=kx经过点E,点F时,k的值即可.
,求出直线y=kx经过点E,点F时,k的值即可.
(1)如图1中,作OH⊥AB于H.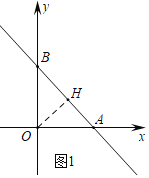
∵A(2,0),B(0,2),
∴OA=OB=2,AB=2![]() ,
,
∵![]() ×OA×OB=
×OA×OB=![]() ×AB×OH,
×AB×OH,
∴OH=![]() ,
,
∴d(点O,直线AB);
(2)如图2中,作TH⊥AB于H,交⊙T于D.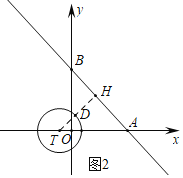
当d(⊙T,直线AB)=1时,DH=1,
∴TH=2,AT=2![]() ,
,
∴OT=2![]() -2,
-2,
∴T(2-2![]() ,0),
,0),
根据对称性可知,当⊙T在直线AB的右边,满足d(⊙T,直线AB)=1时,T(2+2![]() ,0),
,0),
∴满足条件的t的值为2-2![]() ≤t≤2+2
≤t≤2+2![]() .
.
(3)如图3中,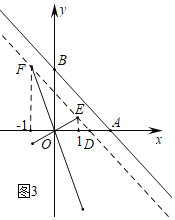
当直线经过点D(2-![]() ,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-
,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-![]() ,
,
当直线y=kx经过E(1,1-![]() )时,k=1-
)时,k=1-![]() ,
,
当直线y=kx经过F(-1,3-![]() ),k=-3+
),k=-3+![]() ,
,
综上所述,满足条件的k的值为-3+![]() 或1-
或1-![]() .
.


科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
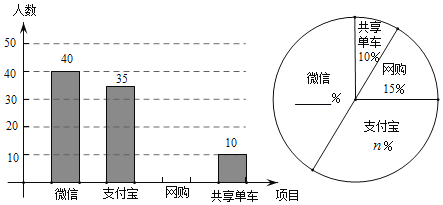
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )
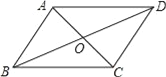
A.AB=ADB.AC⊥BDC.AC=BDD.AD=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
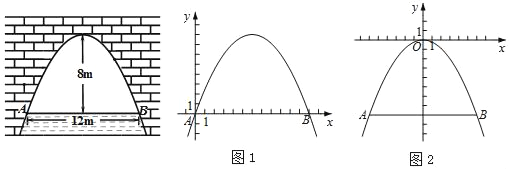
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上,![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.

(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]()
![]() 满足等量关系时,
满足等量关系时,![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中,![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利500元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价10元,商场每天可多售出2件.设每件商品降价x元(x是10的整数倍),据此信息,请回答:
(1)商场日销量增加 件,每件商品盈利 元;(用含x的代数式表示).
(2)在上述条件不变且销售正常的情况下,每件商品降价多少元时,商场日盈利可达到21000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在AC⊥BC,过点C的直线MN∥AB,D为AB边上一点,且AD=4,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求CE的长;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com