
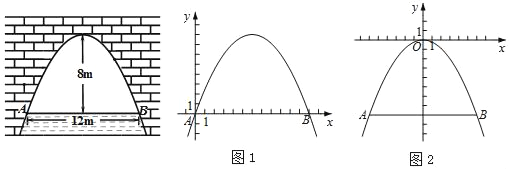
����Ŀ����ͼ�����������ţ���������ˮ��8mʱ��ˮ���ABΪ12m����ˮ������6mʱ�ﵽ����ˮλ����ʱ�����ڵ�ˮ������Ƕ���m��
��������˽�������������ַ������벹��������
����һ����ͼ1���Ե�AΪԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��B������Ϊ���� ������ �����������ߵĶ�������Ϊ���� ������ ������
������������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y��6ʱ�������ʱ�Ա���x��ȡֵ�����ɽ��������⣮
����������ͼ2���������߶���Ϊԭ�㣬�Գ���Ϊy�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y���� ��ʱ�������ʱ�Ա���x��ȡֵΪ�� �������ɽ��������⣮
���𰸡�12��0��6��8��y����![]() x2+
x2+![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��
��������
����һ�������������ʿɵó�B��O���꣬Ȼ������κ����Ľ���ʽΪy��a��x��6��2��8�ٽ�B��������뼴�ɵõ�a��ֵ.
������������κ����Ľ���ʽΪy��ax2��B����뼴�ɵõ�a��ֵ����y����2ʱ���������ʽ���������.
�⣺����һ��B��12��0����O��6��8����
����κ����Ľ���ʽΪy��a��x��6��2��8��
��B����������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��![]() x��
x��
������������κ����Ľ���ʽΪy��ax2��
��B��6����8������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��
y����2ʱ�������ʱ�Ա���x��ȡֵΪ��3��
�ʴ�Ϊ��12��0��6��8��y����![]() x2��
x2��![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�������ͼ��ʾ��ƽ��ֱ������ϵxOy����ABC���������㶼�ڸ���ϣ���A�����꣨4��4���������������⣺
��1��������ABC����y��ԳƵġ�A1B1C1����д����A1��B1��C1�����ꣻ
��2������ABC�Ƶ�C��ʱ����ת90����������ת��ġ�A2B2C2���������A��A2��·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�C.������
��x�ύ�ڵ�A����y�ύ�ڵ�C.������![]() ����A��C���㣬����x�ύ����һ��B����B�ڵ�A�Ҳ�����
����A��C���㣬����x�ύ����һ��B����B�ڵ�A�Ҳ�����

��1���������ߵĽ���ʽ����B���ꣻ
��2������M���߶�BC�ϵ�һ���㣬����M��ֱ��EFƽ��y�ύx���ڵ�F�����������ڵ�E.��ME�������ֵ��
��3����̽����MEȡ���ֵʱ�����������ϡ�x���·��Ƿ���ڵ�P��ʹ��M��F��B��PΪ������ı�����ƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽص��ҵ���������·��һ����ȫ��600km����ͨ��·����һ����ȫ��480km�ĸ��ٹ�·��ij�ͳ��ڸ��ٹ�·����ʻ��ƽ���ٶȱ�����ͨ��·�Ͽ�45![]() /
/![]() ���ɸ��ٹ�·�Ӽص��ҵ������ʱ��������ͨ��·�Ӽص��ҵ�����ʱ���һ�룬��ÿͳ��ɸ��ٹ�·�Ӽص��ҵ������ʱ�䣮
���ɸ��ٹ�·�Ӽص��ҵ������ʱ��������ͨ��·�Ӽص��ҵ�����ʱ���һ�룬��ÿͳ��ɸ��ٹ�·�Ӽص��ҵ������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�ҷ��֣������ϣ�ѧ���Ը���Ľ�������s����������ʱ��t����λ��min��֮��������㺯����ϵs��at2+bt+c��a��0����sֵԽ��ʾ��������Խǿ����ͼ��¼��ѧ��ѧϰij����ʱt��s���������ݣ�������������ģ�ͺ����ݣ����ƶϳ���ѧ������������ǿʱ����������ʱ��Ϊ��������
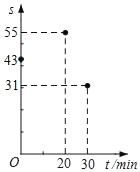
A. 8min B. 13min C. 20min D. 25min
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
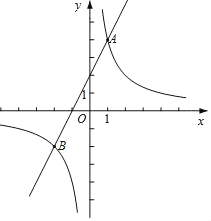
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��2x+2�뺯��y��![]() ��k��0����ͼ����A��B���㣬�ҵ�A������Ϊ��1��m����
��k��0����ͼ����A��B���㣬�ҵ�A������Ϊ��1��m����
��1����k��m��ֵ��
��2����֪��P��a��0��������P��ƽ����y���ֱ�ߣ���ֱ��y��2x+2�ڵ�M��������y��![]() ��k������ͼ���ڵ�N��
��k������ͼ���ڵ�N��
�ٵ�a��2ʱ�����߶�MN�ij���
����PM��PN����Ϻ�����ͼ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
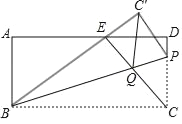
����Ŀ����ͼ���ھ���ABCD�У�AB��6��PΪ��CD��һ�㣬����BCP��ֱ��BP�۵�������C�۵���C'������BC'��AD������E������CE��BP���ڵ�Q����CE��BE��
��1����֤����ABE�ס�DEC��
��2����AD��13ʱ��AE��DE����CE�ij���
��3������C'Q��ֱ��д���ı���C'QCP����״���� ������CP��4ʱ������CEEQ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
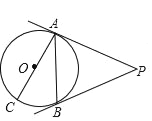
����Ŀ����ͼ��AC����O��ֱ����PA����O�ڵ�A����B����O�ϵ�һ�㣬�ҡ�BAC��30�㣬��APB��60�㣮
��1����֤��PB����O�����ߣ�
��2������O�İ뾶Ϊ2������AB��PA��PB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� x �ĺ��� y=��m��1��x2+2x+m ͼ����������ֻ�� 2 �����㣬��m=_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com