
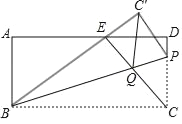
【题目】如图,在矩形ABCD中,AB=6,P为边CD上一点,把△BCP沿直线BP折叠,顶点C折叠到C',连接BC'与AD交于点E,连接CE与BP交于点Q,若CE⊥BE.
(1)求证:△ABE∽△DEC;
(2)当AD=13时,AE<DE,求CE的长;
(3)连接C'Q,直接写出四边形C'QCP的形状: .当CP=4时,并求CEEQ的值.
【答案】(1)见解析;(2)CE=![]() ;(3)菱形,理由见解析
;(3)菱形,理由见解析
【解析】
(1)由题意可得∠AEB+∠CED=90°,且∠ECD+∠CED=90°,可得∠AEB=∠ECD,且∠A=∠D=90°,则可证△ABE∽△DEC;
(2)设AE=x,则DE=13-x,由相似三角形的性质可得![]() ,即:
,即:![]() ,可求x的值,即可得DE=9,根据勾股定理可求CE的长;
,可求x的值,即可得DE=9,根据勾股定理可求CE的长;
(3)由折叠的性质可得CP=C'P,CQ=C'Q,∠C'PQ=∠CPQ,∠BC'P=∠BCP=90°,由平行线的性质可得∠C'PQ=∠CQP=∠CPQ,即可得CQ=CP=C'Q=C'P,则四边形C'QCP是菱形,通过证△C'EQ∽△EDC,可得![]() ,即可求CEEQ的值.
,即可求CEEQ的值.
(1)∵CE⊥BE,
∴∠BEC=90°,
∴∠AEB+∠CED=90°,
又∵∠ECD+∠CED=90°,
∴∠AEB=∠ECD,
又∵∠A=∠D=90°,
∴△ABE∽△DEC;
(2)设AE=x,则DE=13﹣x,
由(1)知:△ABE∽△DEC,
∴![]() ,即:
,即:![]() ,
,
∴x2﹣13x+36=0,
∴x1=4,x2=9,
又∵AE<DE,
∴AE=4,DE=9,
在Rt△CDE中,由勾股定理得:![]() ;
;
(3)∵折叠,
∴CP=C'P,CQ=C'Q,∠C'PQ=∠CPQ,∠BC'P=∠BCP=90°,
∵CE⊥BC',∠BC'P=90°,
∴CE∥C'P,
∴∠C'PQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP,
∴CQ=CP=C'Q=C'P,
∴四边形C'QCP是菱形,
故答案为:菱形;
∵四边形C'QCP是菱形,
∴C'Q∥CP,C'Q=CP,∠EQC'=∠ECD
又∵∠C'EQ=∠D=90°
∴△C'EQ∽△EDC
∴![]() ,
,
即:CEEQ=DCC'Q=6×4=24.


科目:初中数学 来源: 题型:
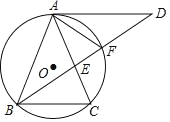
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
(3)求证:AD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
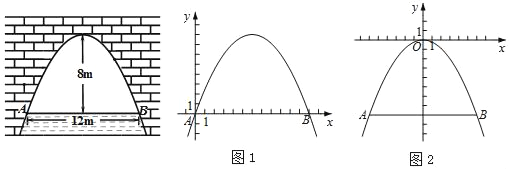
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
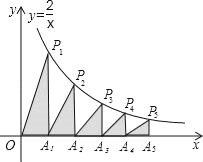
【题目】如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=![]() (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S10=_____.(n≥1的整数)
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S10=_____.(n≥1的整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系中,若x2﹣2![]() x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
(1)求B点的坐标.
(2)把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BD的解析式.
(3)在平面上是否存在点P,使D、C、B、P四点形成的四边形为平形四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )
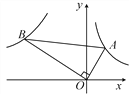
A. -3 B. -4 C. -![]() D. -2
D. -2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
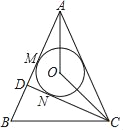
【题目】如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点,⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°;
(2)若NC=3,BC=2![]() ,求DM的长.
,求DM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com