
����Ŀ������������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1��x2+2x+2��y2��x2��2x+2�ǡ�����y��Գƶ��κ�������
��1��ֱ��д������ͼ�С�����y��Գƶ��κ�����ͼ�������еĹ�ͬ�ص㣮
��2�����κ���y��2��x+2��2+1�ġ�����y��Գƶ��κ���������ʽΪ�� �������κ���y��a��x��h��2+k�ġ�����y��Գƶ��κ���������ʽΪ�� ����
��3��ƽ��ֱ������ϵ�У��ǡ�����y��Գƶ��κ�������ͼ����y��Ľ���ΪA�����ǵ���������ֱ�ΪB��C����BC��6��˳�����ӵ�A��B��O��C�õ�һ�����Ϊ24�����Σ�����y��Գƶ��κ������ĺ�������ʽ��
���𰸡���1�������������2��y��2��x��2��2+1��y��a��x+h��2+k����3��y����![]() ��x��3��2��4��
��x��3��2��4��
��������
��1������������y��Գƶ��κ��������ɵô𰸣�
��2������������y��Գƶ��κ��������ɵô𰸣�
��3������������y��Գƶ��κ����������ε�������ɵö������꣬ͼ����y��Ľ��㣬���ݴ���ϵ�������ɵô𰸣�
�⣺��1��ֱ��д������ͼ�С�����y��Գƶ��κ�����ͼ�������еĹ�ͬ�ص�ʱ�������y��Գƣ��Գ������y��Գƣ�
��2�����κ���y��2��x+2��2+1�ġ�����y��Գƶ��κ���������ʽΪ y��2��x��2��2+1��
���κ���y��a��x��h��2+k�ġ�����y��Գƶ��κ���������ʽΪy��a��x+h��2+k��
�ʴ�Ϊ��y��2��x��2��2+1��y��a��x+h��2+k��
��3����ͼ��

��BC��6��˳�����ӵ�A��B��O��C�õ�һ�����Ϊ24�����Σ���
OA��8��A��������0��8����B�����������3��4����
��һ�������ߵĽ���ʽΪy��a��x+3��2+4����A��������룬��
9a+4��8��
���a��![]() ��
��
y��![]() ��x+3��2+4����y��Գƶ��κ����ĺ�������ʽy��
��x+3��2+4����y��Գƶ��κ����ĺ�������ʽy��![]() ��x��3��2+4��
��x��3��2+4��
���ݶԳ��ԣ��������µ�������Ҳ�������⣬
������y��Գƶ��κ������ĺ�������ʽΪy����![]() ��x+3��2��4����y��Գƶ��κ����ĺ�������ʽy����
��x+3��2��4����y��Գƶ��κ����ĺ�������ʽy����![]() ��x��3��2��4��
��x��3��2��4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�ij����Ʒƽ��ÿ�������30����ÿ��ӯ��500Ԫ��Ϊ�˾�����ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣�ÿ����Ʒÿ����10Ԫ���̳�ÿ��ɶ��۳�2������ÿ����Ʒ����xԪ��x��10�������������ݴ���Ϣ����ش�
��1���̳������������� ����ÿ����Ʒӯ���� Ԫ�����ú�x�Ĵ���ʽ��ʾ����
��2��������������������������������£�ÿ����Ʒ���۶���Ԫʱ���̳���ӯ���ɴﵽ21000Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
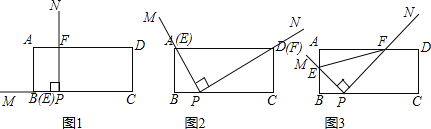
����Ŀ����ͼ����AC��BC������C��ֱ��MN��AB��DΪAB����һ�㣬��AD=4������D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����CE�ij���
��2����D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
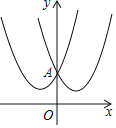
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=![]() x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60��õ���CBD������B������Ϊ��2��0�������C������Ϊ ��
x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60��õ���CBD������B������Ϊ��2��0�������C������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
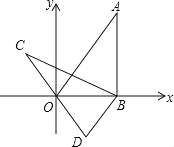
����Ŀ����ͼ����·���£�С����������ͼ���߶�AB��ʾ�����ڵ����ϵ�Ӱ����ͼ���߶�AC��ʾ��С����������ͼ���߶�FG��ʾ��·�Ƶ������߶�DE�ϣ�
��1������ȷ���������ڵ�λ�ã���������ʾС���ڵƹ����γɵ�Ӱ���߶Σ�
��2������Ƹ˸�12m��С��������1.6m��С����Ƹ˵ľ���13m�������С��Ӱ�ӵij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��
��![]() ����ʼ��˳ʱ�뷽����ת��
����ʼ��˳ʱ�뷽����ת��![]() ����
����![]() ����
����![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ��ת��
��ת��![]() ��ʱ��
��ʱ��![]() ֹͣ��ת.
ֹͣ��ת.
��1���������Σ���ͼ2�����ֵ�![]() ����
����![]() ʱ��PNҲǡ�ɹ���
ʱ��PNҲǡ�ɹ���![]() ����ʱ
����ʱ![]()
![]() ����ա��ס�����
����ա��ס�����
��2�����̽������ͼ3������ת�����У�![]() ��ֵ�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵������.
��ֵ�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�BC=6cm������AG��BC����E��A����������AG��1cm/s���ٶ����˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt(s).
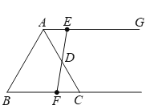
(1)����EF����EF����AC�ߵ��е�D�ǣ���֤��ADE�ա�CDF��
(2)����⣺�ٵ�tΪ________sʱ���ı���ACFE�����Σ�
�ڵ�tΪ________sʱ����A��C��F��EΪ������ı���Ϊƽ���ı���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() ��λ����ͼ��ʾ����ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�
��λ����ͼ��ʾ����ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�
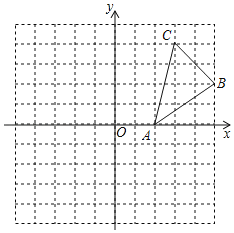
��1������![]() ���ڵ�
���ڵ�![]() �����ĶԳ�ͼ����
�����ĶԳ�ͼ����![]() ��
��
��2����![]() ���ŵ�
���ŵ�![]() ��ʱ����ת
��ʱ����ת![]() ��������ת��õ�����
��������ת��õ�����![]() ��
��
��3�������ø��ͼ�������̶ȵ�ֱ����![]() ���ϵĸ�
���ϵĸ�![]() ��������ͼ�ۼ�����
��������ͼ�ۼ�����
��4��PΪ![]() ����һ�㣬����PBC����BCΪֱ�DZߵ�ֱ�������Σ���ֱ��д����P�����꣮
����һ�㣬����PBC����BCΪֱ�DZߵ�ֱ�������Σ���ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
��ͼ1��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() �ϣ�
�ϣ�![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() .��֤��
.��֤��![]() .
.
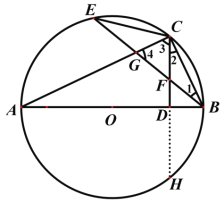
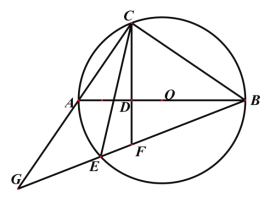
ͼ1 ͼ2
��1������֤����˼·�������п�ͼ��ʾ��
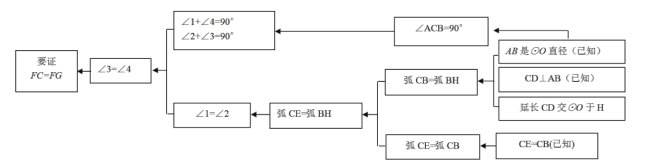
��������˼·��������������д�����֤������.
��2����ͼ2������![]() �͵�
�͵�![]() ��
��![]() �����࣬
�����࣬![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() �������������䣬��1���еĽ��ۻ���������˵�����ɣ�
�������������䣬��1���еĽ��ۻ���������˵�����ɣ�
��3���ڣ�2���������£���![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com