练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在直角梯形ABCD中，AD∥BC，∠B=90度，AC将梯形分成两个三角形，其中△ACD是周长为18cm的等边三角形，则该梯形的中位线的长是（　　）

    A. 9cm B. 12cm C. cm D. 18cm

    【答案】C

    【解析】

    根据等边三角形的三边相等求出边长AD为6cm，再根据三个角都是60°可以求出∠BAC=30°，利用直角三角形30°所对的直角边等于斜边的一半求出BC为3cm，最后根据梯形的中位线等于上底与下底边长和的一半求解即可．

    解：∵△ACD是等边三角形，周长为18cm，
    ∴AD=AC=18÷3=6cm，∠CAD=60°，
    ∵AD∥BC，∠B=90°，
    ∴∠BAC=90°-60°=30°，
    ∴BC=AC=×6=3，
    所以梯形的中位线的长是 =cm．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在规格为8×8的边长为1个单位的正方形网格中（每个小正方形的边长为1），△ABC的三个顶点都在格点上，且直线m、n互相垂直．

    （1）画出△ABC关于直线n的对称图形△A′B′C′；

    （2）直线m上存在一点P，使△APB的周长最小；

    ①在直线m上作出该点P；（保留画图痕迹）

    ②△APB的周长的最小值为　 　．（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC是边长为4cm的等边三角形，边AB在射线OM上，且OA=6cm，点D从点O出发，沿OM的方向以1cm/s的速度运动，当D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．

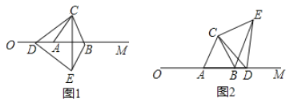
    （1）求证：△CDE是等边三角形（下列图形中任选其一进行证明）；

    （2）如图2，当点D在射线OM上运动时，是否存在以D，E，B为顶点的三角形是直角三角形？若存在，求出运动时间t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y＝2x﹣4的图象分別交x、y轴于点A、B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C，则直线BC的函数表达式是_____．

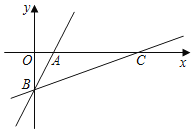
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，和均为等腰直角三角形，，连结，，且、、三点在一直线上，，．

    （1）求证：；

    （2）求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 小明遇到这样一个问题

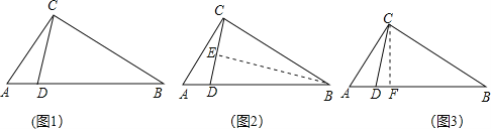
    如图1，△ABC中，∠ACB=90°，点D在AB上，且BD=BC，求证：∠ABC=2∠ACD．

    小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：

    方法2：如图2，作BE⊥CD，垂足为点E．

    方法3：如图3，作CF⊥AB，垂足为点F．

    根据阅读材料，从三种方法中任选一种方法，证明∠ABC=2∠ACD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 在等腰Rt△ABC中，∠C=90°，AC=BC，点M，N分别是边AB，BC上的动点，△BMN与△B′MN关于直线MN对称，点B的对称点为B′．

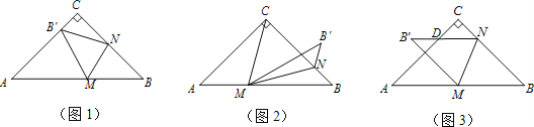
    （1）如图1，当B′在边AC上时，若∠CNB′=25°，求∠AMB′的度数；

    （2）如图2，当∠BMB′=30°且CN=MN时，若CMBC=2，求△AMC的面积；

    （3）如图3，当M是AB边上的中点，B′N交AC于点D，若B′N∥AB，求证：B′D=CN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上的点D处，折痕交OA于点C，则弧AD的长为（　　）

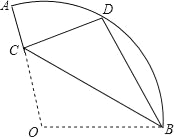
    A. 2π B. 3π C. 4π D. 5π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．阜阳市某家快递公司，2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．

    (1)求该快递公司投递快递总件数的月平均增长率？

    (2) 如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

    查看答案和解析>>

    同步练习册答案