
【题目】已知:如图,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,连结
,连结![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 三点在一直线上,
三点在一直线上,![]() ,
,![]() .
.
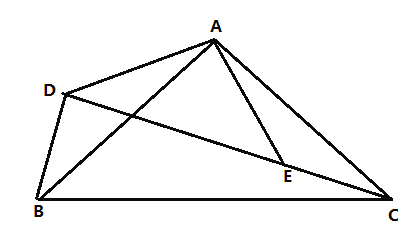
(1)求证:![]() ;
;
(2)求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据等式的基本性质可得∠DAB=∠EAC,然后根据等腰直角三角形的性质可得DA=EA,BA=CA,再利用SAS即可证出结论;
(2)根据等腰直角三角形的性质和勾股定理即可求出DE,从而求出EC和DC,再根据全等三角形的性质即可求出DB,∠ADB=∠AEC,从而求出∠BDC=90°,最后根据勾股定理即可求出结论.
证明:(1)∵![]()
∴∠DAE-∠BAE=∠BAC-∠BAE
∴∠DAB=∠EAC
∵![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
∴DA=EA,BA=CA
在△ADB和△AEC中
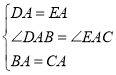
∴△ADB≌△AEC
(2)∵![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴DE=![]() ,
,
∵![]()
∴EC=![]() ,
,
∴DC=DE+EC=3
∵△ADB≌△AEC
∴DB=EC=3,∠ADB=∠AEC
∵∠ADB=∠ADE+∠BDC,∠AEC=∠ADE+∠DAE=∠ADE+90°
∴∠BDC=90°
在Rt△BDC中,![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )
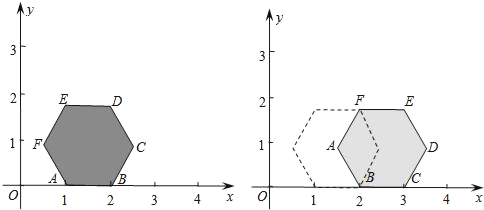
A. (2017,0) B. (2017,![]() )
)
C. (2018,![]() ) D. (2018,0)
) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,BE⊥AC于F,BE交AD于F,BF=AC,
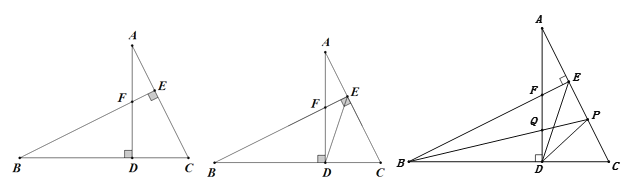
(1)求证:FD=CD;
(2)连DE,求证:ED平分∠BEC;
(3)在(2)条件下,点P在AC上,连BP、DP,BP交AD于Q, BP平分∠EBC,∠BPD=![]() ∠BFD,△APQ的面积为4,求线段PD的长.
∠BFD,△APQ的面积为4,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
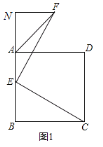
【题目】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.过点F作FN垂直于BA的延长线于点N.
(1)求∠EAF的度数;
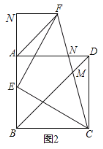
(2)如图2,连接FC交BD于M,交AD于N.猜想BD,AF,DM三条线段的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知A(-1,2),B(-3,1),C(-4,3).
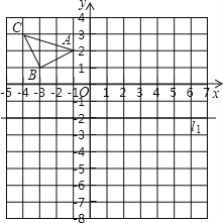
(1)作△ABC关于x轴的对称图形△A1B1C1,写出点C关于x轴的对称点C1的坐标;
(2)作△ABC关于直线l1:y=-2(直线l1上各点的纵坐标都为-2)的对称图形△A2B2C2,写出点C关于直线l1的对称点C2的坐标.
(3)作△ABC关于直线l2:x=1(直线l2上各点的横坐标都为1)的对称图形△A3B3C3,写出点C关于直线l2的对称点C3的坐标.
(4)点P(m,n)为坐标平面内任意一点,直接写出:
点P关于直线x=a(直线上各点的横坐标都为a)的对称点P1的坐标;
点P关于直线y=b(直线上各点的纵坐标都为b)的对称点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离.
(1)写出y与x之间的函数关系式;
(2)当该旅游列车距大同就还有80km时,求行驶了多长时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com