
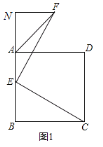
【题目】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.过点F作FN垂直于BA的延长线于点N.
(1)求∠EAF的度数;
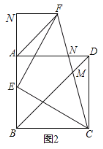
(2)如图2,连接FC交BD于M,交AD于N.猜想BD,AF,DM三条线段的等量关系,并证明.
【答案】(1)∠EAF=135°;(2)BD= AF+2DM,证明见解析
【解析】
(1)证明△EBC≌△FNE,根据全等三角形的对应边相等和正方形的临边相等可证明NA=NF,由此可证△NAF为等腰直角三角形,可求得∠EAF;
(2)过点F作FG∥AB交BD于点G,证明四边形ABGF为平行四边形和△FGM≌△CDM,即可证得结论.
(1)解:∵四边形ABCD是正方形,FN垂直于BA的延长线于点N,
∴∠B=∠N=∠CEF=90°,BC=AB=CD,
∴∠NEF+∠CEB=90°,∠CEB+∠BCE=90°,
∴∠NEF=∠ECB,
∵EC=EF,
∴△EBC≌△FNE,
∴FN=BE, EN=BC ,
∴EN=AB,
∴EN﹣AE=AB﹣AE
∴AN=BE,
∴FN=AN,
∵FN⊥AB,
∴∠NAF=45°,
∴∠EAF=135°.
(2)三条线段的等量关系是BD=AF+2DM.
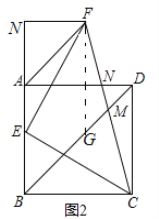
证明:过点F作FG∥AB交BD于点G.
由(1)可知∠EAF=135°,
∵∠ABD=45°
∴∠EAF=135°+∠ABD=180°,
∴AF∥BG,
∵FG∥AB,
∴四边形ABGF为平行四边形,
∴AF=BG,FG=AB,
∵AB=CD,
∴FG=CD,
∵AB∥CD,
∴FG∥CD,
∴∠FGM=∠CDM,
∵∠FMG=∠CMD
∴△FGM≌△CDM,
∴GM=DM,
∴DG=2DM,
∴BD=BG+DG=AF+2DM.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
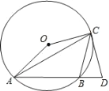
【题目】如图,△ABC是⊙O内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O切线交AB延长线于点D.
(1)求证:CD=CB;(2)如果⊙O的半径为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
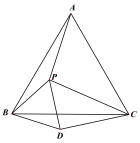
【题目】已知:如图,点P是等边△ABC内的一点,连接PA、PB、PC,以PB为边作等边△BPD,连接CD,若∠APB=150°,BD=6,CD=8,△APB的面积为( ).
A.48B.24C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从点O出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
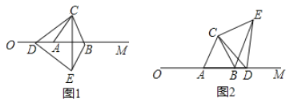
(1)求证:△CDE是等边三角形(下列图形中任选其一进行证明);
(2)如图2,当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出运动时间t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
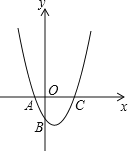
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2,0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2>![]() ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
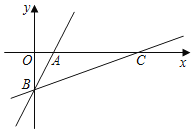
【题目】如图,在平面直角坐标系中,一次函数y=2x﹣4的图象分別交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在等腰Rt△ABC中,∠C=90°,AC=BC,点M,N分别是边AB,BC上的动点,△BMN与△B′MN关于直线MN对称,点B的对称点为B′.
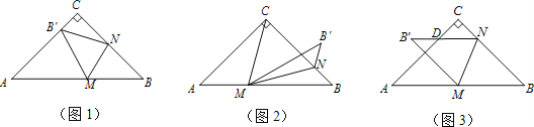
(1)如图1,当B′在边AC上时,若∠CNB′=25°,求∠AMB′的度数;
(2)如图2,当∠BMB′=30°且CN=MN时,若CMBC=2,求△AMC的面积;
(3)如图3,当M是AB边上的中点,B′N交AC于点D,若B′N∥AB,求证:B′D=CN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学连续三年开展植树活动![]() 已知第一年植树500棵,第三年植树720棵,假设该校这两年植树棵数的年平均増长率相同.
已知第一年植树500棵,第三年植树720棵,假设该校这两年植树棵数的年平均増长率相同.
![]() 求这两年该校植树棵数的年平均增长率;
求这两年该校植树棵数的年平均增长率;
![]() 按照
按照![]() 的年平均增长率,预计该校第四年植树多少棵?
的年平均增长率,预计该校第四年植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com