
【题目】 在等腰Rt△ABC中,∠C=90°,AC=BC,点M,N分别是边AB,BC上的动点,△BMN与△B′MN关于直线MN对称,点B的对称点为B′.
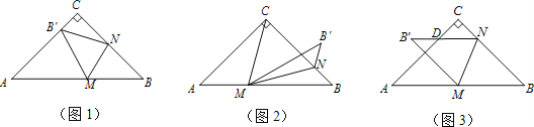
(1)如图1,当B′在边AC上时,若∠CNB′=25°,求∠AMB′的度数;
(2)如图2,当∠BMB′=30°且CN=MN时,若CMBC=2,求△AMC的面积;
(3)如图3,当M是AB边上的中点,B′N交AC于点D,若B′N∥AB,求证:B′D=CN.
【答案】(1)65°;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由△MNB′是由△MNB翻折得到,推出∠B=∠MB′N=45°,∠MNB=∠MNB′=![]() (180°-25°)=77.5°,推出∠NMB=∠NMB′=57.5°,可得∠BMB°=115°解决问题.
(180°-25°)=77.5°,推出∠NMB=∠NMB′=57.5°,可得∠BMB°=115°解决问题.
(2)如图2,作MH⊥AC于H.首先证明![]() ,推出S△ACM=
,推出S△ACM=![]() 即可解决问题.
即可解决问题.
(3)如图3,设AM=BM=a,则AC=BC=![]() a.通过计算证明CN=DB′即可.
a.通过计算证明CN=DB′即可.
(1)如图,
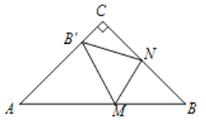
∵∠C=90°,CA=CB,
∴∠A=∠B=45°,
∵△MNB′是由△MNB翻折得到,
∴∠B=∠MB′N =45°,∠MNB=∠MNB′=![]() (180°-25°)=77.5°,
(180°-25°)=77.5°,
∴∠NMB=∠NMB′=57.5°,
∴∠BM B′=115°,
∴∠AMB′=180°-115°=65°;
(2)∵△MNB′是由△MNB翻折得到,∠BMB′=30°,
∴∠BMN=∠NMB′=15°,
∵∠B=45°,
∴∠CNM=∠B+∠NMB=60°,
∵CN=MN,
∴△CMN是等边三角形,
∴∠MCN=60°,
∵∠ACB=90°,
∴∠ACM=30°,
如图,作MH⊥AC于H.
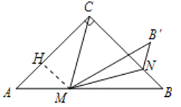
∴∠MHC=90°,
∴MH=![]() CM,
CM,
∵S△ACM=![]() AC
AC![]() MH=
MH=![]() BC
BC![]() CM=
CM=![]() CM
CM![]() BC=
BC=![]() ;
;
(3)如图,设AM=BM=a,则AC=BC=![]() a.
a.
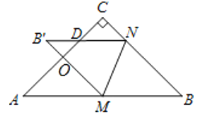
∵NB′∥AB,
∴∠CND=∠B=45°,∠MND=∠NMB,
∵∠MNB=∠MND,
∴∠NMB =∠MNB,
∴MB=BN=a,
∴CN=![]() a-a,
a-a,
∵∠C=90°,
∴∠CDN=∠CND=45°,
∴CD=CN,
∵CA=CB,
∴AD=BN=a,
设AD交MB′于点O,
∵MB=BN,∠B=45°,
∴∠BMN=![]() ,
,
∵△MNB′是由△MNB翻折得到,
∴∠BMN=∠NMB′=![]() ,
,
∴∠AMO=180![]() ∠BMN
∠BMN![]() ∠NMB′=180
∠NMB′=180![]() ,
,
∴![]() 是等腰直角三角形,且AM=a,
是等腰直角三角形,且AM=a,
∴AO=OM=![]() a,OB′=OD=a-
a,OB′=OD=a-![]() a,
a,
∴DB′=![]() OD=
OD=![]() a-a,
a-a,
∴B′D=CN.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
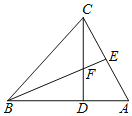
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE的延长线与BD交于点A.
(1)求证:BF=AC;
(2)求证:BE是AC的中垂线;
(3)若BD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
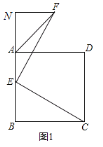
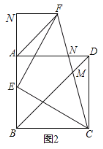
【题目】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.过点F作FN垂直于BA的延长线于点N.
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.猜想BD,AF,DM三条线段的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知A(-1,2),B(-3,1),C(-4,3).
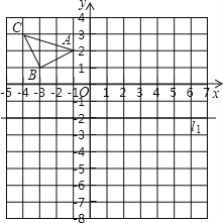
(1)作△ABC关于x轴的对称图形△A1B1C1,写出点C关于x轴的对称点C1的坐标;
(2)作△ABC关于直线l1:y=-2(直线l1上各点的纵坐标都为-2)的对称图形△A2B2C2,写出点C关于直线l1的对称点C2的坐标.
(3)作△ABC关于直线l2:x=1(直线l2上各点的横坐标都为1)的对称图形△A3B3C3,写出点C关于直线l2的对称点C3的坐标.
(4)点P(m,n)为坐标平面内任意一点,直接写出:
点P关于直线x=a(直线上各点的横坐标都为a)的对称点P1的坐标;
点P关于直线y=b(直线上各点的纵坐标都为b)的对称点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离.
(1)写出y与x之间的函数关系式;
(2)当该旅游列车距大同就还有80km时,求行驶了多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com