
【题目】如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从点O出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
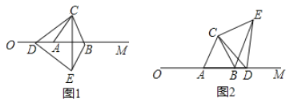
(1)求证:△CDE是等边三角形(下列图形中任选其一进行证明);
(2)如图2,当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出运动时间t的值;若不存在,请说明理由.
【答案】(1)见解析;(2) 存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
【解析】
(1)由旋转的性质可得CD=CE,∠DCA=∠ECB,由等边三角形的判定可得结论;
(2)分四种情况,由旋转的性质和直角三角形的性质可求解.
(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)解:存在,
①当0≤t<6s时,由旋转可知,![]() ,
,![]() ,
,
若![]() ,由(1)可知,△CDE是等边三角形,
,由(1)可知,△CDE是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OD=OA﹣DA=6﹣4=2,
∴t=2÷1=2s;
②当6<t<10s时,由∠DBE=120°>90°,
∴此时不存在;
③ t = 10s时,点D与点B重合,
∴此时不存在;
④ 当t>10s时,由旋转的性质可知, ∠CBE=60°
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4cm,
∴OD=14cm,
∴t=14÷1=14s;
综上所述:当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.


科目:初中数学 来源: 题型:
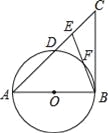
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
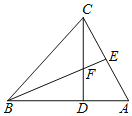
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE的延长线与BD交于点A.
(1)求证:BF=AC;
(2)求证:BE是AC的中垂线;
(3)若BD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,BE⊥AC于F,BE交AD于F,BF=AC,
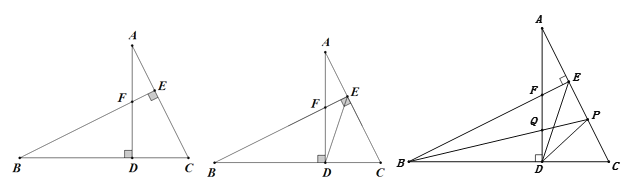
(1)求证:FD=CD;
(2)连DE,求证:ED平分∠BEC;
(3)在(2)条件下,点P在AC上,连BP、DP,BP交AD于Q, BP平分∠EBC,∠BPD=![]() ∠BFD,△APQ的面积为4,求线段PD的长.
∠BFD,△APQ的面积为4,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
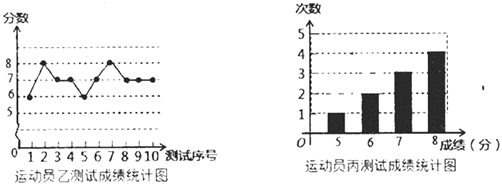
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
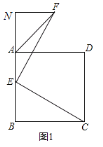
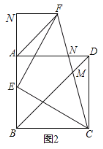
【题目】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.过点F作FN垂直于BA的延长线于点N.
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.猜想BD,AF,DM三条线段的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com