
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的平分线与
的平分线与![]() 的垂直平分线
的垂直平分线![]() 交于点
交于点![]() ,
,![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() .
.
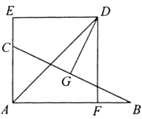
(1)求证:![]() ;
;
(2)求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
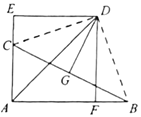
(1)如图,连接![]() ,
,![]() ,根据角平分线的性质可得DE=DF,根据垂直平分线的性质可得DC=DB,利用HL可证明Rt△DEC≌Rt△DFB,即可得EC=BF;
,根据角平分线的性质可得DE=DF,根据垂直平分线的性质可得DC=DB,利用HL可证明Rt△DEC≌Rt△DFB,即可得EC=BF;
(2)根据四边形内角和可得∠EDF=90°,根据全等三角形的性质可得∠EDC=∠FDB,根据角的和差关系可得∠CDB=∠EDF=90°,利用勾股定理可求出BC的长,根据直角三角形斜边中线的性质即可求出DG的长.
(1)连接![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 垂直平分线
垂直平分线![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,∠BAC=90°,DF⊥AB,
,∠BAC=90°,DF⊥AB,
∴![]() -∠BAC=90°,
-∠BAC=90°,
∵Rt△DEC≌Rt△DFB,
∴![]() ,
,
∴![]() ,
,
∴∠CDB=∠EDF=90°,
∵AC=5,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 垂直平分
垂直平分![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
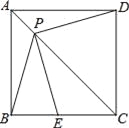
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学连续三年开展植树活动![]() 已知第一年植树500棵,第三年植树720棵,假设该校这两年植树棵数的年平均増长率相同.
已知第一年植树500棵,第三年植树720棵,假设该校这两年植树棵数的年平均増长率相同.
![]() 求这两年该校植树棵数的年平均增长率;
求这两年该校植树棵数的年平均增长率;
![]() 按照
按照![]() 的年平均增长率,预计该校第四年植树多少棵?
的年平均增长率,预计该校第四年植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,连接
上的点,连接![]() ,
,![]() ,
,![]() .
.

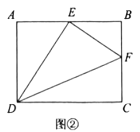
(1)如图①,当![]() 时,试说明
时,试说明![]() 是直角三角形;
是直角三角形;
(2)如图②,若点![]() 是边
是边![]() 的中点,
的中点,![]() 平分
平分![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
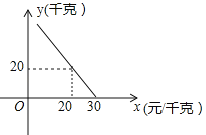
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
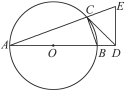
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com