
【题目】已知抛物线![]() 与
与![]() 轴的两个交点间的距离为2.
轴的两个交点间的距离为2.
(1)若此抛物线的对称轴为直线![]() ,请判断点(3,3)是否在此抛物线上?
,请判断点(3,3)是否在此抛物线上?
(2)若此抛物线的顶点为(S,t),请证明![]() ;
;
(3)当![]() 时,求
时,求![]() 的取值范围
的取值范围
【答案】(1)点(3,3)在此抛物线上;(2)见解析;(3)24<b<99.
【解析】
(1)根据已知条件得出两个交点坐标,利用待定系数法求出解析式,然后验证点(3,3)是否在这条抛物线上即可;
(2)先确定对称轴为直线![]() ,再得出与x轴的两交点坐标为(
,再得出与x轴的两交点坐标为(![]() ,0)和(
,0)和(![]() ,0),再利用待定系数法求出解析式的顶点式可得解;
,0),再利用待定系数法求出解析式的顶点式可得解;
(3)把t=-1代入顶点坐标公式,得到二次函数解析式![]() ,根据函数的增减性分别计算a=10和20时b的值从而得解.
,根据函数的增减性分别计算a=10和20时b的值从而得解.
(1)抛物线的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴的两个交点间的距离为2,可得抛物线与
轴的两个交点间的距离为2,可得抛物线与![]() 轴的两个交点为(0,0)和(2,0),
轴的两个交点为(0,0)和(2,0),
所以抛物线![]() 的解析式为与
的解析式为与![]()
当![]() 时,
时,![]()
所以点(3,3)在此抛物线上 .
(2)抛物线的顶点为![]() ,则对称轴为直线
,则对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴的两个交点间的距离为2,
轴的两个交点间的距离为2,
可得抛物线与![]() 轴的两个交点为(
轴的两个交点为(![]() ,,0)和(
,,0)和(![]() ,0)
,0)
所以抛物线![]() 的解析式为与
的解析式为与![]()
由![]() 得
得![]()
所以![]() ;
;
(3)由(2)知![]() 即
即![]() 整理得
整理得![]()
由对称轴为直线![]() ,且二次项系数
,且二次项系数![]()
可知 当![]() 时,b的随a的增大而增大
时,b的随a的增大而增大
当a=10时,得![]()
当a=20时,得![]()
所以 当![]() 时,
时,![]()


科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,进价为每台40元,经市场预测,售价为每台48元时,可售出220台;售价每增加1元,销售量减少10台。
(1)当售价为55元,销售量为多少台?
(2)因受库存的影响,每批次进货个数不得超过160台,若商店想获得2000元利润,则应进货多少台?售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠B=36°,点D为斜边BC的中点,将线段DC绕着点D逆时针旋转任意角度得到线段DE(点E不与A、B、C重合),连接EA,EC,则∠AEC=___________°.
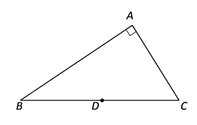
查看答案和解析>>
科目:初中数学 来源: 题型:
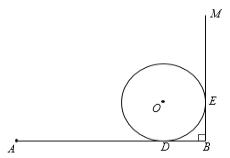
【题目】如图,∠ABM=90°,⊙O分别切AB、BM于点D、E.AC切⊙O于点F,交BM于点C(C与B不重合).
(1)用直尺和圆规作出AC(保留作图痕迹,不写作法);
(2)若⊙O半径为1,AD=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( )
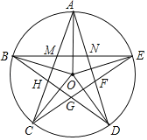
A.① ②B.① ③C.② ③D.① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=16cm,AE=4cm.

(1)求⊙O的半径;
(2)求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交![]() 轴于点B、C.解答下列问题:
轴于点B、C.解答下列问题:
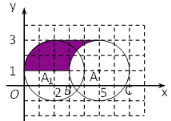
(1)将⊙A向下平移 个单位长度与![]() 轴相切;
轴相切;
(2) 将⊙A向左平移得到⊙A1,当⊙A1与![]() 轴首次相切,此时阴影部分的面积S= ;
轴首次相切,此时阴影部分的面积S= ;
(3)将⊙A向左平移 个单位长度与坐标轴有三个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 ( )
 .
.
A.(-4,3)B.(-3,4)C.(3,-4)D.(4,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.当销售单价为多少时,超市每天销售这种玩具可获利润2250元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com