【题目】如图，二次函数
的图象与x轴交于A、B 两点，与y轴交于点C，且点B的坐标为（1，0），点C的坐标为（0，﹣3），一次函数y2=mx+n的图象过点A、C．
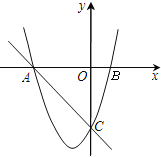
（1）求二次函数的解析式；
（2）求二次函数的图象与x轴的另一个交点A的坐标；
（3）根据图象写出y2＜y1时，x的取值范围．
【答案】(1) 
;(2) 此二次函数的图象与x轴的另一个交点A的坐标为（﹣3，0）;(3) x＜﹣3或x＞0.
【解析】
（1）把B（1，0），C（0，﹣3）分别代入
得到关于b、c的方程组，求出b、c即可；
（2）令y1=0，得到x2+2x﹣3=0，然后解一元二次方程即可得到二次函数的图象与x轴的另一个交点A的坐标；
（3）观察图象可得当x＜﹣3或x＞0，抛物线都在直线的上方，即y2＜y1．
解：（1）由二次函数的图象经过B（1，0）、C （0，﹣3）两点，
得
，
解这个方程组，得
，
∴抛物线的解析式为；
（2）令y1=0，得x2+2x﹣3=0，
解这个方程，得x1=﹣3，x2=1，
∴此二次函数的图象与x轴的另一个交点A的坐标为（﹣3，0）；
（3）当x＜﹣3或x＞0，y2＜y1．
科目：初中数学 来源： 题型：
【题目】闺蜜装在大学校园里盛行，闺蜜装能很好的表达“亲如姐妹”的友谊，也能成为校园一道靓丽的风景.某专卖店购进一批
，
两款闺蜜装，共花费了18400元，款比款多20套，其中每套款闺蜜装进价200元，每套款闺蜜装进价160元.进行试销售，供不应求，很快销售完毕，己知每套款闺蜜装售价为240元.
（1）求购进，两款闺蜜装各多少套？
（2）国庆将至，专卖店又购进第二批，两款闺蜜装并进行促销活动，在促销期间，每套款闺蜜装在进价的基础上提高
销售，每套款闺蜜装在第一批售价的基础上降低
销售，结果在促销售活动中，款闺蜜装的销量比第一批款销售量降低了
，款闺蜜装的销售量比第一批款销售量上升了
，结果本次促销活动共获利5200元，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（定义）从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
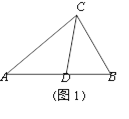
（1）如图1，△ABC中，∠A＝40°，∠B＝60°，CD平分∠ACB．求证：CD为△ABC的完美分割线；
（2）在△ABC中，CD是△ABC的完美分割线，其中△ACD为等腰三角形，设∠A＝x°，∠B＝y°，则y与x之间的关系式为_____________________________；
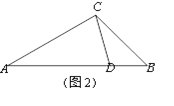
（3）如图2，△ABC中，AC＝2，BC＝
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行调查，随机调查了m人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图．
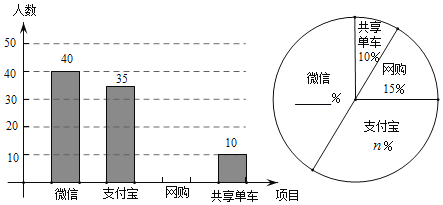
（1）根据图中信息求出m= ，n= ；
（2）请你帮助他们将这两个统计图补全；
（3）根据抽样调查的结果，请估算全校2000名学生中，大约有多少人最认可“微信”这一新生事物？
（4）已知A、B两位同学都最认可“微信”，C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学，请你通过树状图或表格，求出这两位同学最认可的新生事物不一样的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
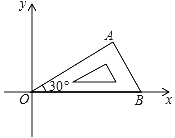
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中，OB 在 x轴上，若 OA＝2，将三角板绕原点 O 顺时针旋转 75°，则点 A 的对应点 A′ 的坐标为___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，对角线AC与BD交于点O，若增加一个条件，使ABCD成为菱形，下列给出的条件不正确的是（ ）
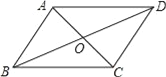
A.AB=ADB.AC⊥BDC.AC=BDD.AD=CD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线型拱桥，当拱顶离水面8m时，水面宽AB为12m．当水面上升6m时达到警戒水位，此时拱桥内的水面宽度是多少m？
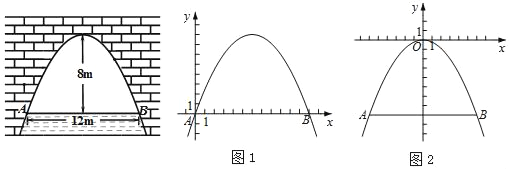
下面给出了解决这个问题的两种方法，请补充完整：
方法一：如图1，以点A为原点，AB所在直线为x轴，建立平面直角坐标系xOy，
此时点B的坐标为（ ， ），抛物线的顶点坐标为（ ， ），
可求这条抛物线所表示的二次函数的解析式为 ．
当y＝6时，求出此时自变量x的取值，即可解决这个问题．
方法二：如图2，以抛物线顶点为原点，对称轴为y轴，建立平面直角坐标系xOy，
这时这条抛物线所表示的二次函数的解析式为 ．
当y＝ 时，求出此时自变量x的取值为 ，即可解决这个问题．
查看答案和解析>>
科目：初中数学 来源： 题型：
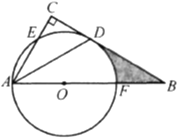
【题目】如图，在△ABC中，∠C = 90°，∠BAC 的平分线交BC于点D，点O在AB上，以点O为圆心、OA长为半径的圆恰好经过点D，分别交AC，AB于点E，F．
(1)试判断直线BC与⊙O的位置关系，并说明理由；
(2)若OA = 2，∠B = 30°，求涂色部分的面积(结果保留
和根号)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com