
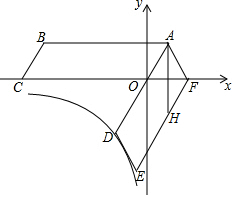
 如图,四边形ABCO是平行四边形且点C(-4,0),将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点A,D在反比例函数y=$\frac{k}{x}$的图象上,过A作AH⊥x轴,交EF于点H.
如图,四边形ABCO是平行四边形且点C(-4,0),将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点A,D在反比例函数y=$\frac{k}{x}$的图象上,过A作AH⊥x轴,交EF于点H.分析 (1)由旋转的性质可知AO=AF,且∠AOF=∠BAO,可证得△AOF为等边三角形,由题意可知A、D关于原点对称,则可求得OA的长,设AH交x轴于点K,则可中求得OK和AK的长,可求得A点坐标,代入反比例函数解析式可求得k的值;
(2)设G(x,0),由A、C的坐标可分别表示出AG、CG和AC的长,分AG=CG、AG=AC和CG=AC三种情况分别得到关于x的方程,可求得x的值,则可求得G点坐标;
(3)把P、Q的坐标代入反比例函数解析式可用x1、x2分别表示出a、b,则可比较m、n的大小关系,利用反比例函数的性质可求得y1,y2的大小.
解答 解:
(1)由旋转的性质可得AO=AF=DE=BC,∠BAO=∠OAF,
∵AB∥BC,
∴∠BAO=∠AOF,
∴∠AOF=∠OAF,
∴AF=OF,
∴AF=OF=OA,
∴△AOF为等边三角形,
∵点A,D在反比例函数y=$\frac{k}{x}$的图象上,
∴A、D关于原点对称,
∴AO=OD=$\frac{1}{2}$AD=$\frac{1}{2}$OC=2,
如图1,设AH交x轴于点K,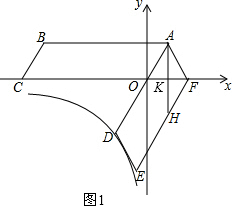
在Rt△AOK中,可得∠OAK=30°,
∴OK=$\frac{1}{2}$OA=1,AK=$\frac{\sqrt{3}}{2}$OA=$\sqrt{3}$,
∴A(1,$\sqrt{3}$),
∴k=1×$\sqrt{3}$=$\sqrt{3}$;
(2)设G(x,0),且A(1,$\sqrt{3}$),C(-4,0),
∴AG=$\sqrt{(x-1)^{2}+(\sqrt{3})^{2}}$=$\sqrt{{x}^{2}-2x+4}$,CG=|x+4|,AC=$\sqrt{(1+4)^{2}+(\sqrt{3})^{2}}$=2$\sqrt{7}$,
∵△ACG是等腰三角形,
∴有AG=CG、AG=AC和CG=AC三种情况,
①当AG=CG时,则$\sqrt{{x}^{2}-2x+4}$=|x+4|,解得x=-$\frac{6}{5}$,此时G点坐标为(-$\frac{6}{5}$,0);
②当AG=AC时,则$\sqrt{{x}^{2}-2x+4}$=2$\sqrt{7}$,解得x=-4(与C点重合,舍去)或x=6,此时G点坐标为(6,0);
③当CG=AC时,则|x+4|=2$\sqrt{7}$,解得x=-4+2$\sqrt{7}$或x=-4-2$\sqrt{7}$,此时G点坐标为(-4+2$\sqrt{7}$,0)或(-4-2$\sqrt{7}$,0);
综上可知G点坐标为(-$\frac{6}{5}$,0)或(6,0)或(-4+2$\sqrt{7}$,0)或(-4-2$\sqrt{7}$,0);
(3)y1<y2.理由如下:
由(1)可知反比例函数解析式为y=$\frac{\sqrt{3}}{x}$,
∵P(x1,a),Q(x2,b)(x2>x1>0)在反比例函数图象上,
∴a=$\frac{\sqrt{3}}{{x}_{1}}$,b=$\frac{\sqrt{3}}{{x}_{2}}$,
∴m=$\sqrt{\frac{a+b}{2k}}$=$\sqrt{\frac{\frac{\sqrt{3}}{{x}_{1}}+\frac{\sqrt{3}}{{x}_{2}}}{2\sqrt{3}}}$=$\sqrt{\frac{{x}_{1}+{x}_{2}}{2{x}_{1}{x}_{2}}}$,
∴m2-n2=$\frac{{x}_{1}+{x}_{2}}{2{x}_{1}{x}_{2}}$-$\frac{2}{{x}_{1}+{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}{2{x}_{1}{x}_{2}({x}_{1}+{x}_{2})}$=$\frac{({x}_{1}-{x}_{2})^{2}}{2{x}_{1}{x}_{2}({x}_{1}+{x}_{2})}$,
∵x2>x1>0,
∴$\frac{({x}_{1}-{x}_{2})^{2}}{2{x}_{1}{x}_{2}({x}_{1}+{x}_{2})}$>0,即m2-n2>0,
∴m2>n2,
又由题意可知m>0,n>0,
∴m>n,
∵M(m,y1),N(n,y2)在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,且在第一象限,
∴y1<y2.
点评 本题为反比例函数的综合应用,涉及待定系数法、平行四边形的性质、旋转的性质、等边三角形的判定和性质、直角三角形的性质、等腰三角形的性质、勾股定理、反比例函数图象的性质、方程思想及分类讨论思想等知识.在(1)中由旋转的性质求得OA=AF=OF是解题的关键,在(2)中用G点坐标分别表示出GC、AG和AC的长是解题的关键,注意分情况讨论,在(3)中比较出m、n的大小关系是解题的关键.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | 增加了10% | B. | 减少了10% | C. | 增加了(1+10%) | D. | 没有改变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
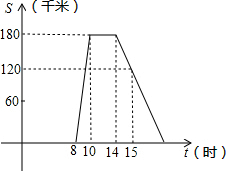 某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t(时)的关系可以用如图的折线表示.根据图象提供的有关信息,得到以下四个结论,其中正确的结论有( )个.
某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t(时)的关系可以用如图的折线表示.根据图象提供的有关信息,得到以下四个结论,其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(-a+b) | B. | (a+b)(-a-b) | C. | (a+b)(b+a) | D. | (a-b)(b-a) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
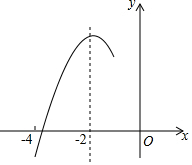 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点(-$\frac{9}{2}$,y1),(-$\frac{5}{2}$,y2),(-$\frac{1}{2}$,y3)是该抛物线上的点,则y1<y2<y3,正确的个数有( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点(-$\frac{9}{2}$,y1),(-$\frac{5}{2}$,y2),(-$\frac{1}{2}$,y3)是该抛物线上的点,则y1<y2<y3,正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
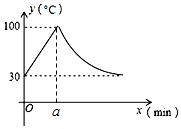 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com