
【题目】我们学过角的平分线的概念.类比给出新概念:从一个角的顶点出发,把这个角分成![]() 的两个角的射线,叫做这个角的三分线.显然,一个角的三分线有两条,例如:如图1,若
的两个角的射线,叫做这个角的三分线.显然,一个角的三分线有两条,例如:如图1,若![]() ,则
,则![]() 是
是![]() 的一条三分线.
的一条三分线.
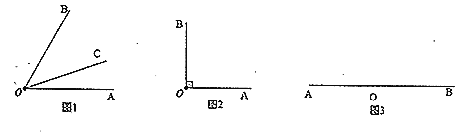
(1)如图1,若![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若![]() ,若
,若![]() 是
是![]() 的两条三分线.
的两条三分线.
①求![]() 的度数;
的度数;
②现以O为中心,将![]() 顺时针旋转
顺时针旋转![]() 度(
度(![]() )得到
)得到![]() ,当
,当![]() 恰好是
恰好是![]() 的三分线时,则求
的三分线时,则求![]() 的值.
的值.
(3)如图3,若![]() ,
,![]() 是
是![]() 的一条三分线,
的一条三分线,![]() 分别是
分别是![]() 与
与![]() 的平分线,将
的平分线,将![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,若射线
的速度沿顺时针方向旋转一周,在旋转的过程中,若射线![]() 恰好是
恰好是![]() 的三分线,则此时
的三分线,则此时![]() 绕点
绕点![]() 旋转的时间是多少秒?(直接写出答案即可,不必说明理由)
旋转的时间是多少秒?(直接写出答案即可,不必说明理由)
【答案】(1)![]() ;(2)①
;(2)①![]() ,②40或50;(3)25,26,28或29秒
,②40或50;(3)25,26,28或29秒
【解析】
(1)由OC是∠AOB的一条三分线,且![]() ,即可求解;
,即可求解;
(2)①由![]() 是
是![]() 的两条三分线,可得
的两条三分线,可得![]() ,即可求解;②以O为中心,将∠COD顺时针旋转n度(n<360°)得到
,即可求解;②以O为中心,将∠COD顺时针旋转n度(n<360°)得到![]() ,当OA恰好是
,当OA恰好是![]() 的三分线时,分两种情况:当OA是
的三分线时,分两种情况:当OA是![]() 的三分线,且
的三分线,且![]() 时;当OA是
时;当OA是![]() 的三分线,且
的三分线,且![]() 时,分别求解即可;
时,分别求解即可;
(3)由OC是∠AOB的一条三分线,![]() ,得
,得![]() 或
或![]() ,分两种情况讨论:当
,分两种情况讨论:当![]() 时;当
时;当![]() 时,分别求出∠MON绕点O沿顺时针方向旋转的度数,进而即可求解.
时,分别求出∠MON绕点O沿顺时针方向旋转的度数,进而即可求解.
(1)∵OC是∠AOB的一条三分线,且![]() ,
,
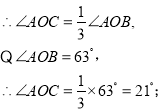
(2)①![]() 是
是![]() 的两条三分线,
的两条三分线,
![]() ;
;
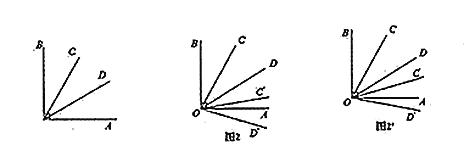
②现以O为中心,将∠COD顺时针旋转n度(n<360°)得到![]() ,当OA恰好是
,当OA恰好是![]() 的三分线时,分两种情况:
的三分线时,分两种情况:
当OA是![]() 的三分线,且
的三分线,且![]() 时,如图2,
时,如图2,
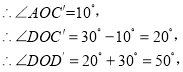
当OA是![]() 的三分线,且
的三分线,且![]() 时,如图2',
时,如图2',
![]()
![]()
![]()
∴n=40或50;
(3)∵OC是∠AOB的一条三分线,![]() ,
,
∴![]() 或
或![]() ,
,
∵OM,ON分别是∠AOC与∠BOC的平分线,
∴![]() ,
,
当![]() 时,如图3,
时,如图3,
∵60°+180°+20°=260°或60°+180°+40°=280°,
∴∠MON绕点O沿顺时针方向旋转260°或280°时,ON是∠AOC的一条三分线,
∴![]() (秒)或
(秒)或![]() (秒);
(秒);
当![]() 时,如图3′,
时,如图3′,
∵30°+180°+40°=250°或30°+180°+80°=290°,
∴![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 或
或![]() 时,
时,![]() 是
是![]() 的一条三分线,
的一条三分线,
∴![]() (秒)或
(秒)或![]() (秒)
(秒)
综上,![]() 绕点
绕点![]() 沿顺时针方向旋转的时间是25,26,28或29秒.
沿顺时针方向旋转的时间是25,26,28或29秒.


科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 是正方形,点 E,F 分别在 BC,CD 上,点 G 在 CD 的延长线上,且 BE=CF=DG 以线段AE,AG 为两邻边作 AEHG.
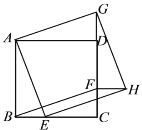
(1)求证:四边形 BEHF 是平行四边形.
(2)若四边形 ABCD 与 AEHG 的面积分别为 16,18.试求四边形 BEHF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李家住房结构如图所示,小李打算把卧室和客厅铺上木地板.
(1)请问他至少需要买多少平方米的木地板?(用字母表示)
(2)若![]() 米,
米,![]() 米时,并且每平方米木地板的价格是
米时,并且每平方米木地板的价格是![]() 元,则他至少需要准备多少元钱?
元,则他至少需要准备多少元钱?
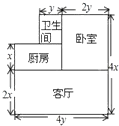
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
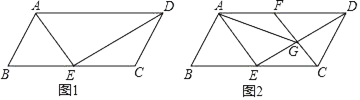
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离![]() (千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
(千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
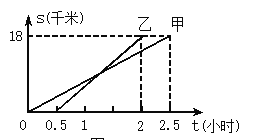
A. 乙比甲早出发半小时 B. 乙在行驶过程中没有追上甲
C. 乙比甲先到达B地 D. 甲的行驶速度比乙的行驶速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中A(1,1)、B(4,4)、C(5,1).
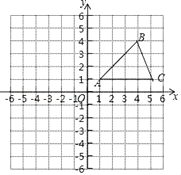
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△A2B2C2,A、B、C的对应点分别是A2、B2、C2;
(3)连CB2,直接写出点B2、C2的坐标B2: 、C2: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G
(1)判断BE与AF的位置关系,并说明理由;
(2)若∠BEC=15°,求四边形BCEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图、点A、B分别为抛物线![]() 、
、![]() 与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线
与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线 ![]() 、
、![]() 上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
(1)求b和c的值
(2)求以A、B、P、Q为顶点的四边形是平行四边形时m的值。
( 3 )当m为何值是,线段PQ的长度取的最大值?并求出这个最大值。
(4)直接写出线段PQ的长度随m增大而减小的m的取值范围。
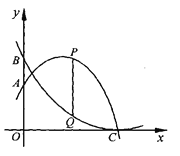
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
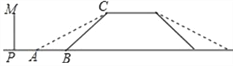
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com