
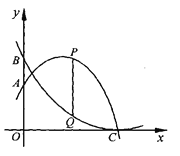
【题目】如图、点A、B分别为抛物线![]() 、
、![]() 与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线
与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线 ![]() 、
、![]() 上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
(1)求b和c的值
(2)求以A、B、P、Q为顶点的四边形是平行四边形时m的值。
( 3 )当m为何值是,线段PQ的长度取的最大值?并求出这个最大值。
(4)直接写出线段PQ的长度随m增大而减小的m的取值范围。
【答案】(1)![]() ,
, ![]() .(2)m值为
.(2)m值为![]() 或
或![]() .(3)
.(3)![]() .(4)
.(4)![]() ≤m<6.
≤m<6.
【解析】整体分析:
(1)把C(6,0)分别代入以这两条抛物线的解析式中,求b,c;(2)分别用含m的代数式表示出点P,Q的纵坐标和PQ的长,用AB=PQ列方程求解;(3)用配方法求PQ的最大值;(4)根据二次函数的性质和x的取值范围求解.
解:(1)∵两条抛物线都经过点C(6,0),
∴![]() ,解得
,解得![]() .
.
![]() ,解得
,解得![]() .
.
(2)根据题意,点A的坐标为(0,4),点B的坐标为(0,6),
∴AB![]() 2.
2.
∵点P的横坐标为m,
∴P(m, ![]() ).
).
∵PQ平行于y轴,∴Q(m, ![]() ).
).
∴PQ=![]()
![]() .
.
∴当![]() 时,
时, ![]() .
.
解得![]() ,
,![]() .
.
∴以A、B、P、Q为顶点的四边形是平行四边形时,
m值为![]() 或
或![]() .
.
(3)由(2)知,PQ=![]() ,
,
∴当m=![]() 时,线段PQ的长度最大,线段PQ的最大长度为
时,线段PQ的长度最大,线段PQ的最大长度为![]() .
.
(4)线段PQ的长度随m的增大而减小的取值范围是![]() ≤m<6
≤m<6


科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元。第二个月商场搞促销活动,将商品的进价加10%作为销售价,第二个月的销售量比第一个月增加了100件,并且商场第二个月比第一个月多获利2000元。问此商品进价是多少元?商场第二个月共销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过角的平分线的概念.类比给出新概念:从一个角的顶点出发,把这个角分成![]() 的两个角的射线,叫做这个角的三分线.显然,一个角的三分线有两条,例如:如图1,若
的两个角的射线,叫做这个角的三分线.显然,一个角的三分线有两条,例如:如图1,若![]() ,则
,则![]() 是
是![]() 的一条三分线.
的一条三分线.
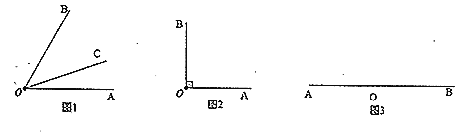
(1)如图1,若![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若![]() ,若
,若![]() 是
是![]() 的两条三分线.
的两条三分线.
①求![]() 的度数;
的度数;
②现以O为中心,将![]() 顺时针旋转
顺时针旋转![]() 度(
度(![]() )得到
)得到![]() ,当
,当![]() 恰好是
恰好是![]() 的三分线时,则求
的三分线时,则求![]() 的值.
的值.
(3)如图3,若![]() ,
,![]() 是
是![]() 的一条三分线,
的一条三分线,![]() 分别是
分别是![]() 与
与![]() 的平分线,将
的平分线,将![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,若射线
的速度沿顺时针方向旋转一周,在旋转的过程中,若射线![]() 恰好是
恰好是![]() 的三分线,则此时
的三分线,则此时![]() 绕点
绕点![]() 旋转的时间是多少秒?(直接写出答案即可,不必说明理由)
旋转的时间是多少秒?(直接写出答案即可,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
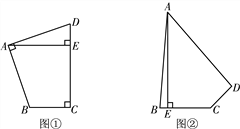
【题目】探究:如图①, 在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E.若AE=10,求四边形ABCD的面积.
应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E.若AE=19,BC=10,CD=6,则四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与合并同类项:
(1)+4.7+(﹣4)﹣2.7﹣(﹣3.5)
(2)11÷(﹣22)﹣3×(﹣11)
(3)16+(﹣2)3+|﹣7|+(![]() )×(﹣4)
)×(﹣4)
(4)0.25×(﹣2)2﹣[﹣4÷(![]() )2+1]÷(﹣1)2020
)2+1]÷(﹣1)2020
(5)5x4+3x2y﹣10﹣3x2y+x4﹣1
(6)(7y﹣3z)﹣(8y﹣5z)
(7)2(2a2+9b)+3(﹣5a2﹣6b)
(8)﹣3(2x2﹣xy)﹣4(x2﹣xy﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b=d(n).
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)= .
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n); d(![]() )=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(
)=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(![]() )= ,d(
)= ,d(![]() )= .
)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com