
【题目】如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
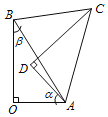
A.α=βB.α=2βC.α+β=90°D.α+β=180°
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲,乙两个工程队分别同时开挖两条 600 m 长的隧道,所挖遂道长度 y(m)与挖掘时间x(天)之间的函数关系如图所示.则下列说法中,错误的是( )
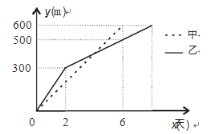
A.甲队每天挖 100 m
B.乙队开挖两天后,每天挖50米
C.甲队比乙队提前2天完成任务
D.当![]() 时,甲、乙两队所挖管道长度相同
时,甲、乙两队所挖管道长度相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
(1)如图1,点![]() 在线段
在线段![]() 上从点
上从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,过点
的速度运动,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,同时点
,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线以
的延长线以![]() 的速度运动,连接
的速度运动,连接![]() 、
、![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①求证:![]() 是等边三角形;
是等边三角形;
②当点![]() 不与点
不与点![]() 、
、![]() 重合时,求证:
重合时,求证:![]() .
.
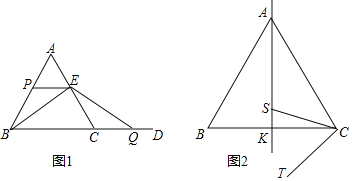
(2)如图2,点![]() 为
为![]() 的中点,作直线
的中点,作直线![]() ,点
,点![]() 为直线
为直线![]() 上一点,连接
上一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,则点
,则点![]() 在直线
在直线![]() 上运动的过程中,
上运动的过程中,![]() 的最小值是多少?请说明理由.
的最小值是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教用品商店欲购进![]() 、
、![]() 两种笔记本,用
两种笔记本,用![]() 元购进的
元购进的![]() 种笔记本与用
种笔记本与用![]() 元购进的
元购进的![]() 种笔记本的数量相同,每本
种笔记本的数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵
种笔记本的进价贵![]() 元.
元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店![]() 种笔记本每本售价
种笔记本每本售价![]() 元,
元,![]() 种笔记本每本售价
种笔记本每本售价![]() 元,准备购进
元,准备购进![]() 、
、![]() 两种笔记本共
两种笔记本共![]() 本,且这两种笔记本全部售出后总获利不小于
本,且这两种笔记本全部售出后总获利不小于![]() 元,则最多购进
元,则最多购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 小明遇到这样一个问题
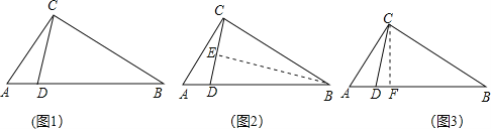
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com