
如图,已知点E,F分别是□ABCD的边BC,AD上的中点,且∠BAC=90°.
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
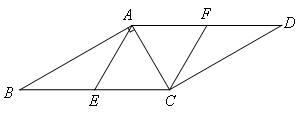
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE=CE=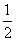 BC.
BC.
同理,AF=CF=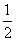 AD.
AD.
∴AF=CE.…………………………………………………………………………………………1
∴四边形AECF是平行四边形.
∴平行四边形AECF是菱形.……………………………………………………………………2
(2)解:在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10,
 ∴AC=5,AB=
∴AC=5,AB=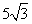 .……………………………………………………………………………3
.……………………………………………………………………………3
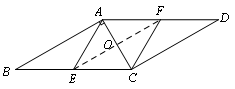
连接EF交于点O,
∴AC⊥EF于点O,点O是AC中点.
∴OE=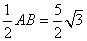 .
.
∴EF=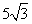 .………………………………………………4
.………………………………………………4
∴菱形AECF的面积是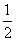 AC·EF=
AC·EF=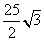 .……………………………………………………5
.……………………………………………………5


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
对某一种四边形给出如下定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.则∠C= 度,∠D=  度.
度.
(2)在探究“等对角四边形”性质时:
小红画了一个“等对角四边形ABCD”(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
(3)已知:在“等对角 四边形ABCD”中,∠DAB=60°,
四边形ABCD”中,∠DAB=60°, ∠ABC=90°,AB=5,AD=4.求对角线AC的长.
∠ABC=90°,AB=5,AD=4.求对角线AC的长.
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com