
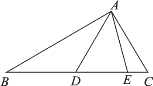
【题目】已知,如图点![]() 在三角形
在三角形![]() 的边
的边![]() 上,且
上,且![]()

(1)求证:![]() ;
;
(2)若![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]()
(3)在(2)的条件下,设![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)(2)见解析(3)3
【解析】
(1)根据∠AEB=∠EBC+∠C、∠ABC=∠EBC+∠ABE和∠AEB=∠ABC,即可求得∠ABE=∠C;
(2)易证∠ADF=∠ABF和∠ADF=∠ABF,即可证明△BAF≌△DAF,
(3)根据全等的性质可得AD=AB,即可解题;
(1)证明:∵∠AEB=∠ABC,
且∠AEB=∠EBC+∠C,∠ABC=∠EBC+∠ABE,
∴∠EBC+∠C=∠EBC+∠ABE,
∴∠ABE=∠C;
(2)解:∵∠BAE的平分线AF交BE于F,
∴∠BAF=∠DAF,
∵FD∥BC交AC于D,
∴∠ADF=∠C,
∵∠ABE=∠C,
∴∠ADF=∠ABE,即∠ADF=∠ABF,
在△BAF和△DAF中,
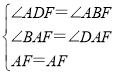 ,
,
∴![]() (AAS),
(AAS),
(3)∵![]()
∴AD=AB=5,
∴DC=ACAD=85=3.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.
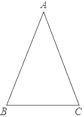
(1)利用尺规作图作边BC的高AD,垂足为D(保留作图痕迹,不写作法);
(2)求证:BD=CD.
(3)如果三角形的周长是22,一边长为5,求它的另外两边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算 27a8 ![]() a3 9a 2 的顺序不正确的是( )
a3 9a 2 的顺序不正确的是( )
A.(27 ![]() 9)a83 2B.(27a8
9)a83 2B.(27a8 ![]() a3 ) 9a 2
a3 ) 9a 2
C.27a8 (![]() a3 9a 2 )D.(27a8 9a 2 )
a3 9a 2 )D.(27a8 9a 2 ) ![]() a3
a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G吗?为什么?
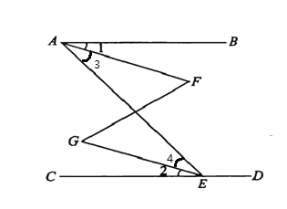
解:因为∠BAE+∠AED=180°( 已知)
所以AB∥CD________
所以∠BAE=∠AEC________
因为∠1=∠2( 已知)
所以∠BAE—∠1=∠AEC—∠2(等式性质)
即∠3=∠4
所以AF∥EG________,
所以∠F=∠G________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线, BA2是∠A1BD的角平分线,CA2 是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3 是∠A2CD的角平分线,若∠A= α,则∠A2019=______________.
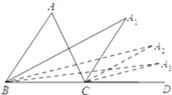
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )

A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在△DAE中, ∠DAE=40°, B、C两点在直线DE上,且∠BAE=∠BEA,∠CAD=∠CDA,则∠BAC的大小是( )
A.100°B.90°C.80°D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com