
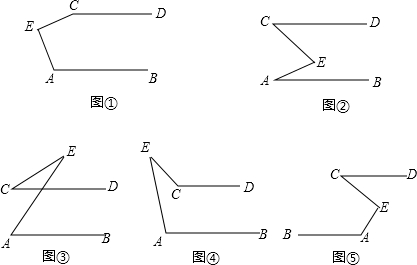
分析 分别过点E作EF∥AB,然后根据平行线的性质表示出∠AEF和∠CEF,再求解即可.
解答 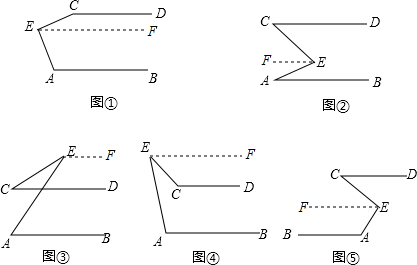 解:过点E作EF∥AB,
解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
如图①,∠AEF=180°-∠A,∠CEF=180°-∠C,
∵∠AEF+∠CEF=180°-∠A+180°-∠C,
∴∠E=360°-∠A-∠C,
∴∠A+∠E+∠C=360°;
如图②,∠AEF=∠A,∠CEF=∠C,
∵∠E=∠AEF+∠CEF,
∴∠E=∠A+∠C;
如图③,∠AEF=180°-∠A,∠CEF=180°-∠C,
∵∠E=∠CEF-∠AEF,
∴∠E=(180°-∠C)-(180°-∠A)=∠A-∠C;
如图④,∠AEF=180°-∠A,∠CEF=180°-∠C,
∵∠E=∠AEF-∠CEF,
∴∠E=(180°-∠A)-(180°-∠C)=∠C-∠A;
如图⑤,∠AEF=180°-∠A,∠CEF=∠C,
∵∠E=∠AEF+∠CEF,
∴∠E=(180°-∠A)+∠C=180°-∠A+∠C,
∴∠A+∠E-∠C=180°.
点评 本题考查了平行线的性质,熟记性质是解题的关键,此类题目,难点在于过拐点E作平行线.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
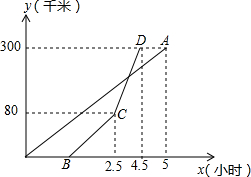 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
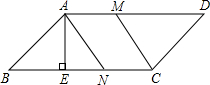 如图,平行四边形ABCD中,AD=9cm,CD=3$\sqrt{2}$cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
如图,平行四边形ABCD中,AD=9cm,CD=3$\sqrt{2}$cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 度数相等的弧是等弧 | |
| C. | 三点确定一个圆 | |
| D. | 圆周角是直角所对弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com