
【题目】(10分)如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.
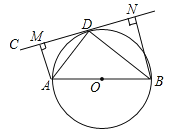
(1)求证:∠ADC=∠ABD;
(2)求证:AD2=AMAB;
(3)若AM=![]() ,sin∠ABD=
,sin∠ABD=![]() ,求线段BN的长.
,求线段BN的长.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)连接OD,由切线的性质和圆周角定理即可得到结果;
(2)证明△ADM∽△ABD,即可得到结论;
(3)根据三角函数和勾股定理即可得到结果.
试题解析:(1)连接OD,∵直线CD切⊙O于点D,∴∠CDO=90°,∵AB为⊙O的直径,∴∠ADB=90°,∴∠1+∠2=∠2+∠3=90°,∴∠1=∠3,∵OB=OD,∴∠3=∠4,∴∠ADC=∠ABD;
(2)∵AM⊥CD,∴∠AMD=∠ADB=90°,∵∠1=∠4,∴△ADM∽△ABD,∴![]() ,∴AD2=AMAB;
,∴AD2=AMAB;
(3)∵sin∠ABD=![]() ,∴sin∠1=
,∴sin∠1=![]() ,∵AM=
,∵AM=![]() ,∴AD=6,∴AB=10,∴BD=
,∴AD=6,∴AB=10,∴BD=![]() =8,∵BN⊥CD,∴∠BND=90°,∴∠DBN+∠BDN=∠1+∠BDN=90°,∴∠DBN=∠1,∴sin∠NBD=
=8,∵BN⊥CD,∴∠BND=90°,∴∠DBN+∠BDN=∠1+∠BDN=90°,∴∠DBN=∠1,∴sin∠NBD=![]() ,∴DN=
,∴DN=![]() ,∴BN=
,∴BN=![]() =
=![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
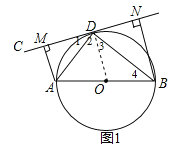
【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形![]() 的四边
的四边![]() 、
、![]() 、
、![]() 、
、![]() 分别延长至
分别延长至![]() 、
、![]() 、
、![]() 、
、![]() ,使得
,使得![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1) 求证:四边形![]() 为平行四边形;
为平行四边形;
(2) 若矩形![]() 是边长为1的正方形,且
是边长为1的正方形,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
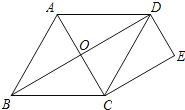
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
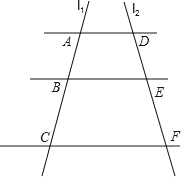
【题目】如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若![]() ,AC=14,
,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
⑴ 随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)
⑵ 小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com